Fourierova transformace

Tento článek potřebuje úpravy.

Můžete Wikipedii pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl, Encyklopedický styl a Odkazy.

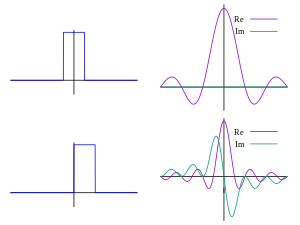
Fourierova transformace je integrální transformace sloužící k dekompozici funkce do jejich frekvenčních komponentů, tj. funkcí ${\displaystyle \sin }$ a ${\displaystyle \cos }$, obecně tedy funkcí komplexní exponenciály. Často se používá k převedení signálu z časové oblasti (funkce času) do oblasti frekvenční (funkce frekvence).

Fourierova transformace převádí mapuje spojitou funkci na spojitou funkci ${\displaystyle s(t)\rightarrow S(\omega )}$. V tom se liší od Fourierovy řady, která převede funkci spojitou na reprezentaci diskrétní, tj. ${\displaystyle s(t)\rightarrow c_{n}}$. Funkce ${\displaystyle S(\omega )}$ reprezentuje amplitudu komplexní exponenciely s frekvencí ${\displaystyle \omega }$.

Příklad využítí Fourierovy transformace je dekompozice zvukové vlny hudebního akordu na zvukovou intenzitu podél frekvence. Pomocí inverzní Fourierovy transformace lze provést opačnou operaci. Zvolením intenzit na různých frekvencích lze vytvořit reprezentaci akordu (nebo jakéhokoliv jiného zvuku), která se pak převede do zvukového signálu, který lze reprodukovat.

Historie

V roce 1822 Joseph Fourier přišel s tvrzením, že jakákoliv funkce, spojitá či nespojitá, je rozepsatelná do řady sínů ^[1].

Spojitý čas

Definice

Fourierova transformace ${\displaystyle S(\omega )}$ funkce ${\displaystyle s(t)}$ je definována integrálním vztahem

${\displaystyle S(\omega )=\int \limits _{-\infty }^{\infty }s(t){\mathrm {e} }^{-{\mathrm {i} }\omega t}\,{\mathrm {d} }t}$

Funkci ${\displaystyle s(t)}$ vypočteme z ${\displaystyle S(\omega )}$ inverzní Fourierovou transformací

${\displaystyle s(t)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }S(\omega ){\mathrm {e} }^{{\mathrm {i} }\omega t}\,{\mathrm {d} }\omega }$

Nevlastní integrály chápeme ve smyslu Cauchyovy hlavní hodnoty, tj.

${\displaystyle \int \limits _{-\infty }^{\infty }[.]\,{\mathrm {d} }=\lim _{T\to \infty }\int \limits _{-T}^{T}[.]\,{\mathrm {d} }}$

Dvojice ve Fourierově transformaci se nazývají originál (zde ${\displaystyle s(t)}$) a obraz (zde ${\displaystyle S(\omega )}$). Vztah mezi originálem a obrazem vyjadřujeme zápisem

${\displaystyle S(\omega )={\mathcal {F}}[s(t)]}$ a ${\displaystyle s(t)={\mathcal {F}}^{-1}[S(\omega )]}$.

V technické oblasti je ${\displaystyle \omega }$ úhlová frekvence, ${\displaystyle S(\omega )}$ představuje spektrum signálu ${\displaystyle s(t)}$.

Spektrum je komplexní veličina a lze vyjádřit ve tvaru ${\displaystyle S(\omega )=\left|S(\omega )\right|{\mathrm {e} }^{{\mathrm {i} }\mathrm {arg} \,S(\omega )}}$. Velikost ${\displaystyle \left|S(\omega )\right|}$ nazýváme amplitudové spektrum a úhel ${\displaystyle {\mbox{arg}}\,S(\omega )}$ fázové spektrum signálu.

Vlastnosti Fourierovy transformace

Věta o linearitě

Lineární kombinaci signálů odpovídá lineární kombinace jejich spekter

${\displaystyle {\mathcal {F}}\left[\sum _{i}c_{i}s_{i}(k)\right]=\sum _{i}c_{i}{\mathcal {F}}[s_{i}(k)]}$

Věta o změně měřítka (Podobnost)

Má-li signál ${\displaystyle s(t)}$ spektrum ${\displaystyle S(\omega )}$, má signál ${\displaystyle s(at),a\neq 0}$ spektrum

${\displaystyle {\frac {1}{\left|a\right|}}S\left({\frac {\omega }{a}}\right)}$.

Tedy rozšíření signálu v časové oblasti odpovídá zúžení ve spektrální oblasti a naopak.

Posun signálu v čase (Posunutí)

Má-li signál ${\displaystyle s(t)}$ spektrum ${\displaystyle S(\omega )}$, má signál zpožděný o veličinu ${\displaystyle a}$ spektrum

${\displaystyle {\mathcal {F}}[s(t-a)]={\mathrm {e} }^{-{\mathrm {i} }\omega a}S(\omega )}$

Amplitudové spektrum posunutého signálu se nemění, mění se jen fázové spektrum a to přímo úměrně zpoždění a kmitočtu. Na rozdíl od věty o translaci v Laplaceově transformaci platí věta pro libovolné a, tedy i pro ${\displaystyle a<0}$.

Spektrum reálného signálu

Je-li signál reálný, pak pro jeho spektrum platí:

• amplitudové spektrum je sudou funkcí^[2]
• fázové spektrum je lichou funkcí^[2]
• spektrum sudého signálu je sudou reálnou funkcí
• spektrum lichého signálu je lichou ryze imaginární funkcí

Diskrétní čas

Definice

Fourierova transformace ${\displaystyle S(\Omega )}$ posloupnosti ${\displaystyle s(k)}$ je definována vztahem

${\displaystyle S(\Omega )=\sum _{k=-\infty }^{\infty }s(k){\mathrm {e} }^{-{\mathrm {i} }\Omega k}}$

Posloupnost ${\displaystyle s(k)}$ vypočteme z ${\displaystyle S(\Omega )}$ inverzní Fourierovou transformací

${\displaystyle s(k)={\frac {1}{2\pi }}\int \limits _{0}^{2\pi }S(\Omega ){\mathrm {e} }^{{\mathrm {i} }\Omega k}\,{\mathrm {d} }\Omega }$

Někteří autoři označují tuto transformaci DtFT (discrete-time Fourier transformation), aby ji odlišili od Fourierovy transformace spojitého signálu. Zde nebudeme značením nijak odlišovat Fourierovu transformaci spojitého a diskrétního signálu. Vztah mezi signálem a jeho spektrem budeme tedy značit

${\displaystyle S(\Omega )={\mathcal {F}}[s(k)]}$ a

${\displaystyle s(k)={\mathcal {F}}^{-1}[S(\Omega )]}$.

Spektrum diskrétního signálu se od spektra spojitého signálu liší tím, že je periodické s periodou ${\displaystyle 2\pi }$.

Diskrétní Fourierova transformace

Definiční vztahy Fourierovy transformace vyžadují znalost matematického vyjádření signálu či spektra. Pokud však zpracováváme naměřené hodnoty, tj. známe vzorky signálu či spektra z konečného intervalu, stojíme před problémem, jak určit spektrum z vzorků signálu či signál ze vzorků spektra. K tomu účelu používáme numerické metody, která je známa jako diskrétní Fourierova transformace (DFT).

Diskrétní Fourierova transformace mezi posloupnostmi ${\displaystyle \{d(k)\}_{k=0}^{N-1}}$, ${\displaystyle \{D(n)\}_{n=0}^{N-1}}$, je definována vztahy:

• přímá diskrétní Fourierova transformace

${\displaystyle D(n)=\sum _{k=0}^{N-1}d(k){\mathrm {e} }^{-{\mathrm {i} }nk2\pi /N},n=0,...,N-1}$

• a zpětná (inverzní) diskrétní Fourierova transformace

${\displaystyle d(k)={\frac {1}{N}}\sum _{n=0}^{N-1}D(n){\mathrm {e} }^{{\mathrm {i} }nk2\pi /N},k=0,...,N-1}$

Diskrétní Fourierova transformace našla velké uplatnění zejména s rozvojem výpočetní techniky. Součástí řady přístrojů jsou jednoúčelové procesory realizující tuto transformaci. Výpočet DFT podle definičního vztahu vyžaduje ${\displaystyle N^{2}}$ komplexních součinů a ${\displaystyle N^{2}}$ komplexních součtů. Toto množství operací výrazně snižovalo možnost aplikace DFT na výpočty v reálném čase.

Situace se změnila po roce 1965, kdy J. W. Cooley a J. W. Tukey popsali velmi efektivní algoritmus výpočtu DFT, tzv. rychlou Fourierovu transformaci (FFT – Fast Fourier Transform), který vyžaduje jen ${\displaystyle N\log _{2}N}$ komplexních součinů a ${\displaystyle N\log _{2}N}$ komplexních součtů. Díky tomuto algoritmu se stala diskrétní Fourierova transformace nejrozšířenějším prostředkem pro numerický výpočet Fourierovy transformace. Algoritmus FFT je také implementován ve všech nejrozšířenějších matematických programech jako je např. GNU Octave, Mathcad, Mathematica, Maple, Matlab atd.

Diskrétní Fourierova transformace se dá vyjádřit jako násobení vektoru ${\displaystyle d_{n}}$ Vandermondovou maticí, která která obsahuje komplexní odmocniny z 1.

Zpětná Fourierova transformace

${\displaystyle f(t)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }S(\omega ){\mathrm {e} }^{{\mathrm {i} }\omega t}\,{\mathrm {d} }\omega }$

Integrál je nutno chápat ve smyslu hlavní hodnoty. Popisuje význam F. t. - rozklad obecného (i neperiodického) signálu f(t) na směs harmonických kmitů, jejichž amplituda je daná amplitudovým spektrem a fázový posun fázovým spektrem.

Související články

• Fourierova řada
• Diskrétní kosinová transformace
• Rychlá Fourierova transformace

Reference

Externí odkazy

• Obrázky, zvuky či videa k tématu Fourierova transformace na Wikimedia Commons
• Václav Hlaváč: LINEÁRNÍ INTEGRÁLNÍ TRANSFORMACE - Fourierova transformace, Fakulta elektrotechnická ČVUT v Praze, katedra kybernetiky, Centrum strojového vnímání
• FOURIEROVA TRANSFORMACE M. Hušek, P. Pyrih et al., Matematicko-fyzikální fakulta, Univerzita Karlova v Praze
• Fourierova transformace - názorné vysvětlení
• Fourier Series 3D - interaktivní demonstrace principu Fourierových řad HTML5 a JavaScript: Unikátní interaktivní 3D zobrazení propojující časovou, frekvenční, amplitudovou a fázovou osu.