Heronův vzorec

Heronův vzorec je vzorec pro výpočet obsahu obecného trojúhelníku (v eukleidovské rovině) pomocí délek jeho stran.

Pokud 3 kladná čísla splňují trojúhelníkovou nerovnost, existuje v eukleidovské rovině (podle věty sss) až na polohu a orientaci jediný trojúhelník s těmito délkami stran. Takže je jednoznačně určen i jeho obsah a je tedy funkcí stran. Ta musí být obecně symetrická a kvadraticky homogenní a H. v. ukazuje, jak přesně vypadá.

Vzorec

Jsou-li a , b , c {\displaystyle a,b,c} délky stran trojúhelníka, platí pro jeho obsah

S = s ( s − a ) ( s − b ) ( s − c ) , {\displaystyle S={\sqrt {s(s-a)(s-b)(s-c)}},}

kde s = a + b + c 2 {\displaystyle s={\frac {a+b+c}{2}}} je poloviční obvod trojúhelníku.

Důkaz

Heronův vzorec lze odvodit již na základní škole, spočívá na Pythagorově větě.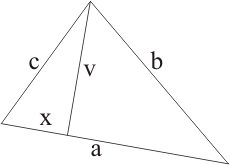

Označme x vzdálenost vrcholu B od paty kolmice z vrcholu A na stranu a (výšky). Pro pravoúhlý trojúhelník na obrázku platí:

  x 2 + v 2 = c 2 {\displaystyle \ x^{2}+v^{2}=c^{2}}

  ( a − x ) 2 + v 2 = b 2 {\displaystyle \ (a-x)^{2}+v^{2}=b^{2}}

Odečteme-li od druhé rovnice první, dostaneme:

  a 2 − 2 a x = b 2 − c 2 {\displaystyle \ a^{2}-2ax=b^{2}-c^{2}}

Z tohoto vztahu vyjádříme x:

x = a 2 + c 2 − b 2 2 a {\displaystyle x={\frac {a^{2}+c^{2}-b^{2}}{2a}}}

Toto platí i v pravoúhlém trojúhelníku, v tupoúhlém s opačným znaménkem. Jestliže za x dosadíme do první rovnice, získáme výšku v:

  v 2 = c 2 − x 2 {\displaystyle \ v^{2}=c^{2}-x^{2}}

v 2 = c 2 − ( a 2 + c 2 − b 2 2 a ) 2 {\displaystyle v^{2}=c^{2}-\left({\frac {a^{2}+c^{2}-b^{2}}{2a}}\right)^{2}}

v 2 = c 2 − ( a 2 + c 2 − b 2 ) 2 4 a 2 {\displaystyle v^{2}=c^{2}-{\frac {\left(a^{2}+c^{2}-b^{2}\right)^{2}}{4a^{2}}}}

v 2 = 4 c 2 a 2 − ( a 2 + c 2 − b 2 ) 2 4 a 2 {\displaystyle v^{2}={\frac {4c^{2}a^{2}-\left(a^{2}+c^{2}-b^{2}\right)^{2}}{4a^{2}}}}

v = 4 c 2 a 2 − ( a 2 + c 2 − b 2 ) 2 2 a {\displaystyle v={\frac {\sqrt {4c^{2}a^{2}-\left(a^{2}+c^{2}-b^{2}\right)^{2}}}{2a}}}

Dosadíme-li tuto výšku do vzorce pro obsah trojúhelníku

S = a v 2 , {\displaystyle S={\frac {av}{2}},}

dostaneme

S = 4 c 2 a 2 − ( a 2 + c 2 − b 2 ) 2 4 {\displaystyle S={\frac {\sqrt {4c^{2}a^{2}-\left(a^{2}+c^{2}-b^{2}\right)^{2}}}{4}}}

Dále pomocí rozkladů upravíme výraz pod odmocninou:

S = ( 2 a c + a 2 + c 2 − b 2 ) ( 2 a c − a 2 − c 2 + b 2 ) 4 {\displaystyle S={\frac {\sqrt {\left(2ac+a^{2}+c^{2}-b^{2}\right)\left(2ac-a^{2}-c^{2}+b^{2}\right)}}{4}}}

S = [ ( a + c ) 2 − b 2 ] [ b 2 − ( a − c ) 2 ] 4 {\displaystyle S={\frac {\sqrt {\left[\left(a+c\right)^{2}-b^{2}\right]\left[b^{2}-\left(a-c\right)^{2}\right]}}{4}}}

S = ( a + c + b ) ( a + c − b ) ( b + a − c ) ( b − a + c ) 4 {\displaystyle S={\frac {\sqrt {\left(a+c+b\right)\left(a+c-b\right)\left(b+a-c\right)\left(b-a+c\right)}}{4}}}

Dosadíme poloviční obvod s,

  a + b + c = 2 s {\displaystyle \ a+b+c=2s}

a dostáváme výsledný vzorec:

S = 2 s ( 2 s − 2 a ) ( 2 s − 2 b ) ( 2 s − 2 c ) 4 {\displaystyle S={\frac {\sqrt {2s\left(2s-2a\right)\left(2s-2b\right)\left(2s-2c\right)}}{4}}}

S = 16 s ( s − a ) ( s − b ) ( s − c ) 4 {\displaystyle S={\frac {\sqrt {16s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}{4}}}

S = s ( s − a ) ( s − b ) ( s − c ) {\displaystyle S={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}}

Historie

Vzorec byl formulován Hérónem z Alexandrie a důkaz byl publikován v jeho knize Métrika, napsané v první polovině 1. století.[1]

Poznámky

Kratší důkaz je možný pomocí kosinové věty.

Díky trojúhelníkové nerovnosti jsou všechny činitele odmocněnce H. v. kladné.

Jedná se asi o nejsložitější matematický vzorec základní školy.

Heronův vzorec je limitním případem Brahmaguptova vzorce pro obsah tětivového čtyřúhelníku.

Reference

  1. ↑ http://mathworld.wolfram.com/HeronsFormula.html

Související články

Externí odkazy

  • Logo Wikimedia Commons Obrázky, zvuky či videa k tématu Heronův vzorec na Wikimedia Commons
  • důkaz Heronova vzorce