Metoda nejmenších čtverců

Tento článek potřebuje úpravy.

Můžete Wikipedii pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl, Encyklopedický styl a Odkazy.

Metoda nejmenších čtverců je matematicko-statistická metoda pro aproximaci řešení přeurčených soustav rovnic (tj. soustav, kde je více rovnic, než neznámých). „Nejmenší čtverce“ znamenají, že výsledné řešení má minimalizovat součet čtverců odchylek vůči každé rovnici. Metoda je v základní podobě určená pro řešení nekompatibilních soustav lineárních rovnic (v obecnější podobě hovoříme o nelineární metodě nejmenších čtverců), díky čemuž je fakticky ekvivalentní tzv. lineární regresi.

S nejjednodušší aplikací metody nejmenších čtverců se setkáváme například při prokládání (aproximaci) naměřených jednorozměrných dat přímkou. Nepatrně složitější aplikací je proložení dat parabolou, obecným polynomem předem daného stupně, nebo obecnou lineární kombinací předem daných bázových funkcí. Fakt, že proložení dat polynomem libovolného, ale předem daného stupně je stále lineární regresí, je častým zdrojem nedorozumění a terminologických nejasností. Další jednoduchou aplikací je nalezení nejpravděpodobnějšího průsečíku několika přímek (jejichž matematický popis je zatížen chybou) v rovině. Metoda nejmenších čtverců má velmi mnoho dalších aplikací v nejširším okruhu vědních oborů, ve kterých se setkáváme s nepřesnými daty, od statistiky a ekonomie, přes geodézii až po zpracování signálů a teorii řízení.

Obecně metoda nejmenších čtverců slouží k eliminaci chyb, kterou provádí optimálně vzhledem k pevně danému jednoznačnému kritériu (viz níže). Optimálně eliminovat chyby v datech lze i vzhledem k jiným kriteriím, takový postup může vést na metody převoditelné na metodu nejmenších čtverců (při použití různých typů vážení, např. když je známo, že chyba některých měření se výrazně liší od zbytku), nebo na metody obecně nepřevoditelné (nebo obtížně převoditelné) na metodu nejmenších čtverců (např. úplný problém nejmenších čtverců).^[1]

Historie

Metodu nejmenších čtverců poprvé použil Carl Friedrich Gauss v roce 1795 pro eliminaci chyb při geodetickém vyměřování.

Odvození metody

Uvažujme lineární aproximační problém

${\displaystyle {\mathbf {A}}{\mathbf {x}}\approx {\mathbf {b}},\qquad {\mathbf {A}}\in \mathbb {R} ^{n\times m},\quad {\mathbf {x}}\in \mathbb {R} ^{m},\quad {\mathbf {b}}\in \mathbb {R} ^{n}}$

takový, že ${\displaystyle {\mathbf {b}}\not \in {\mathcal {R}}({\mathbf {A}})}$ (jinými slovy, neexistuje žádný vektor ${\displaystyle {\mathbf {x}}}$ takový, aby nastala rovnost); symbol ${\displaystyle {\mathcal {R}}({\mathbf {A}})}$ značí obor hodnot matice ${\displaystyle {\mathbf {A}}}$, tedy lineární obal jejích sloupců. Metoda nejmenších čtverců hledá vektor ${\displaystyle {\mathbf {x}}_{LS}}$ (LS je zkratkou anglického least squares) splňující

${\displaystyle \|{\mathbf {A}}{\mathbf {x}}_{LS}-{\mathbf {b}}\|_{2}=\min _{{\mathbf {x}}\in \mathbb {R} ^{m}}\|{\mathbf {A}}{\mathbf {x}}-{\mathbf {b}}\|_{2},}$

nebo ekvivalentně, opravu pravé strany ${\displaystyle {\mathbf {e}}_{LS}}$ splňující

${\displaystyle \|{\mathbf {e}}_{LS}\|_{2}=\min _{{\mathbf {e}}\in \mathbb {R} ^{n}}\|{\mathbf {e}}\|_{2},\quad {\text{kde}}\quad ({\mathbf {b}}+{\mathbf {e}})\in {\mathcal {R}}({\mathbf {A}}).}$

Zřejmě ${\displaystyle {\mathbf {A}}{\mathbf {x}}_{LS}={\mathbf {b}}+{\mathbf {e}}_{LS}}$ a oprava pravé strany ${\displaystyle {\mathbf {e}}={\mathbf {A}}{\mathbf {x}}-{\mathbf {b}}}$ je residuum odpovídající vektoru ${\displaystyle {\mathbf {x}}}$. Označíme-li ${\displaystyle e_{1},\ldots ,e_{n}}$ jednotlivé komponenty vektoru ${\displaystyle {\mathbf {e}}}$, pak z definice Eukleidovské normy přímo plyne

${\displaystyle \|{\mathbf {A}}{\mathbf {x}}-{\mathbf {b}}\|_{2}=\|{\mathbf {e}}\|_{2}=(\sum _{j=1}^{n}e_{j}^{2})^{1/2}\qquad \Longleftrightarrow \qquad \|{\mathbf {A}}{\mathbf {x}}-{\mathbf {b}}\|_{2}^{2}=\|{\mathbf {e}}\|_{2}^{2}=\sum _{j=1}^{n}e_{j}^{2}.}$

Takže minimalizujeme součet čtverců jednotlivých komponent vektoru ${\displaystyle {\mathbf {e}}}$, tj. odchylek jednotlivých komponent pravé strany ${\displaystyle {\mathbf {b}}}$. Nalezení vztahu pro vektor ${\displaystyle {\mathbf {x}}_{LS}}$ splňující podmínku minimality můžeme provést buď pomocí derivací (hledáním lokálního extrému) nebo přímo pomocí Pythagorovy věty.

Minimalizace kvadratického funkcionálu: Residuum ${\displaystyle {\mathbf {e}}={\mathbf {A}}{\mathbf {x}}-{\mathbf {b}}}$ je vektor, jehož normu minimalizujeme. Zřejmě

${\displaystyle \arg \min \|{\mathbf {e}}\|_{2}=\arg \min \|{\mathbf {e}}\|_{2}^{2},\quad {\text{kde}}\quad \|{\mathbf {e}}\|_{2}^{2}={\mathbf {e}}^{T}{\mathbf {e}}=\sum e_{j}^{2},}$

Úlohu tedy můžeme zapsat jako minimalizaci kvadratického funkcionálu, kde volné parametry minimalizace jsou komponenty vektoru ${\displaystyle {\mathbf {x}}}$. Lokální extrém funkcionálu leží v bodě, kde se derivace funkcionálu podle všech komponent vektoru ${\displaystyle {\mathbf {x}}}$ rovnají nule. Z vlastností normy je zřejmé, že se jedná o lokální minimum, které je zároveň minimem globálním. V maticovém zápisu lze formálně použít derivaci podle vektoru ${\displaystyle {\mathbf {x}}}$. Dostáváme

${\displaystyle \left({\mathbf {e}}^{T}{\mathbf {e}}\right)'=\left[\left({\mathbf {Ax-b}}\right)^{T}\left({\mathbf {Ax-b}}\right)\right]'=\left[{\mathbf {x}}^{T}{\mathbf {A}}^{T}{\mathbf {Ax}}-{\mathbf {x}}^{T}{\mathbf {A}}^{T}{\mathbf {b}}-{\mathbf {b}}^{T}{\mathbf {Ax}}+{\mathbf {b}}^{T}{\mathbf {b}}\right]'=2{\mathbf {A}}^{T}{\mathbf {Ax}}-2{\mathbf {A}}^{T}{\mathbf {b}}=0.}$

Ortogonalita: Hledáme vektor ${\displaystyle {\mathbf {e}}}$ s minimální normou, tj. eukleidovskou délkou. Z Pythagorovy věty vyplývá, že nejkratší vzdálenost dostaneme tehdy, pokud bude residuum ${\displaystyle {\mathbf {e}}}$ ortogonální na obor hodnot ${\displaystyle {\mathcal {R}}({\mathbf {A}})}$. Minimality tedy dosáhneme požadavkem

${\displaystyle {\mathbf {e}}\perp {\mathcal {R}}({\mathbf {A}})\qquad \Longleftrightarrow \qquad {\mathbf {A}}^{T}{\mathbf {e}}=0.}$

Dosazením za residuum dostáváme

${\displaystyle {\mathbf {A}}^{T}({\mathbf {A}}{\mathbf {x}}-{\mathbf {b}})={\mathbf {A}}^{T}{\mathbf {A}}{\mathbf {x}}-{\mathbf {A}}^{T}{\mathbf {b}}=0.}$

V obou případech tedy dostáváme, že hledaný vektor ${\displaystyle {\mathbf {x}}_{LS}}$ je řešením tzv. normální soustavy rovnic

${\displaystyle {\mathbf {A}}^{T}{\mathbf {Ax}}={\mathbf {A}}^{T}{\mathbf {b}}.}$

Za předpokladu, že ${\displaystyle {\mathbf {A}}}$ má lineárně nezávislé sloupce (ekvivalentně, že ${\displaystyle {\mathbf {A}}^{T}{\mathbf {A}}}$ je regulární), pak

${\displaystyle {\mathbf {x}}_{LS}=\left({\mathbf {A}}^{T}{\mathbf {A}}\right)^{-1}{\mathbf {A}}^{T}{\mathbf {b}},}$

Z předpokladu lineární nezávislosti sloupců přímo plyne, že řešení je jednoznačné.

Při praktickém výpočtu se ovšem normální soustava nikdy nesestavuje z důvodů numerické stability výpočtu. Použití zde odvozených vztahů pro praktický netriviální výpočet je jen obtížně ospravedlnitelné.^[2]

Pokud má matice ${\displaystyle {\mathbf {A}}}$ lineárně závislé sloupce, je situace nepatrně komplikovanější. Řešení ve smyslu nejmenších čtverců tak jak je definované není jednoznačné. Zpravidla se pak uvažuje řešení ve smyslu nejmenších čtverců minimální v normě. Tedy mezi všemi přípustnými řešeními se hledá řešení s nejmenší normou. Opět užitím Pythagorovy věty můžeme minimalitu normy nahradit ortogonalitou. Řešení minimální v normě je pak ortogonální na nulový prostor matice ${\displaystyle {\mathcal {N}}({\mathbf {A}})}$. Je tedy dáno vztahem

${\displaystyle {\mathbf {x}}_{LS}={\mathbf {A}}^{\dagger }{\mathbf {b}},}$

kde ${\displaystyle {\mathbf {A}}^{\dagger }}$ je Mooreova–Penroseova pseudoinverze. V tomto kontextu je třeba zmínit, že určení (numerické) hodnosti matice, tj. faktu, zda jsou sloupce matice ${\displaystyle {\mathbf {A}}}$ (numericky) lineárně nezávisle, je samo o sobě velmi obtížná úloha.

V následujících odstavcích se seznámíme s nejdůležitějšími aplikacemi metody nejmenších čtverců, vesměs se však jedná pouze o návody jak sestavit matici ${\displaystyle {\mathbf {A}}}$ a pravou stranu ${\displaystyle {\mathbf {b}}}$ v konkrétních případech.

Řešení úlohy nejmenších čtverců

Metod k nalezení řešení ${\displaystyle {\mathbf {x}}_{LS}}$ pro daný aproximační problém ${\displaystyle {\mathbf {A}}{\mathbf {x}}\approx {\mathbf {b}}}$ je celá řada a dají se rozdělit podle dvou zásadních kritérií:

• velikost (a řídkost) problému (za velké považujeme zpravidla takové problémy, kdy s maticí ${\displaystyle {\mathbf {A}}}$ nelze z paměťových a časových důvodů pracovat jako s polem obsahujícím všech ${\displaystyle mn}$ čísel, u reálných problémů mohou být rozměry matic v řádech stovek milionů i vyšší),
• hodnost matice ${\displaystyle {\mathbf {A}}}$, neboli počet lineárně nezávislých sloupců (pokud má matice lineárně závislé sloupce je řešení výrazně komplikovanější).^[2][3]

QR rozklad

Mezi základní metody řešení patří QR rozklad (počítaný buď ortogonálními transformacemi, nebo Gram-Schmidtovým ortogonalizačním procesem). Předpokládejme, že matice ${\displaystyle {\mathbf {A}}}$ má lineárně nezávislé sloupce, pak existuje QR rozklad ve tvaru

${\displaystyle {\mathbf {Q}}{\mathbf {R}}=[{\mathbf {A}},{\mathbf {b}}],\qquad {\mathbf {Q}}=[{\mathbf {Q}}_{1},{\mathbf {q}}_{m+1}]\in \mathbb {R} ^{n\times (m+1)},\quad {\mathbf {R}}=\left[{\begin{array}{cc}{\mathbf {R}}_{1,1}&{\mathbf {r}}_{1,m+1}\\&\rho _{m+1,m+1}\end{array}}\right]\in \mathbb {R} ^{(m+1)\times (m+1)}}$

kde ${\displaystyle {\mathbf {Q}}}$ má ortonormální sloupce, ${\displaystyle {\mathbf {Q}}^{T}{\mathbf {Q}}={\mathbf {I}}_{m}}$ a ${\displaystyle {\mathbf {R}}}$ je horní trojúhelníková. Zřejmě platí ${\displaystyle {\mathbf {A}}={\mathbf {Q}}_{1}{\mathbf {R}}_{1,1}}$ a ${\displaystyle {\mathbf {b}}={\mathbf {Q}}_{1}{\mathbf {r}}_{1,m+1}+{\mathbf {q}}_{m+1}\rho _{m+1,m+1}}$. Formálním dosazením do normální soustavy rovnic dostáváme

${\displaystyle {\mathbf {R}}_{1,1}^{T}{\mathbf {R}}_{1,1}{\mathbf {x}}={\mathbf {R}}_{1,1}^{T}{\mathbf {r}}_{1,m+1}.}$

Po vynásobení maticí ${\displaystyle {\mathbf {R}}_{1,1}^{-T}}$ zleva vidíme, že

${\displaystyle {\mathbf {x}}_{LS}={\mathbf {R}}_{1,1}^{-1}{\mathbf {r}}_{1,m+1}.}$

Řešení tedy dostaneme snadno řešením soustavy s horní trojúhelníkovou maticí ${\displaystyle {\mathbf {R}}_{1,1}}$ (ta je mimochodem Choleského faktorem matice ${\displaystyle {\mathbf {A}}^{T}{\mathbf {A}}}$ ovšem spočteným numericky stabilní cestou).

Výpočet je použitelný pouze pokud má matice ${\displaystyle {\mathbf {A}}}$ (numericky) lineárně nezávislé sloupce (postup lze rozšířit i pro matice s lineárně závislými sloupci pomocí tzv. RRQR rozkladu, obecně tak získáme pouze aproximaci řešení). Matice ${\displaystyle {\mathbf {Q}}}$ při nalezení vlastního řešení potřeba není, můžeme tedy bez problémů použít levnější (ovšem méně přesný) Gram-Schmidtův proces. Pro rozsáhlé úlohy s velkým počtem sloupců může snadno dojít k rychlému zaplnění trojúhelníkového faktoru, proto je tento postup pro tyto typy úloh prakticky nepoužitelný.

Nebezpečí skryté v postupu hledání řešení problému nejmenších čtverců pomocí explicitního sestavení matice ${\displaystyle {\mathbf {A}}^{T}{\mathbf {A}}}$ je dobře známe, viz např. Lauchliho matice.^[4]

Singulární rozklad

Má-li matice ${\displaystyle {\mathbf {A}}}$ lineárně závislé sloupce, jedinou spolehlivou metodou je singulární rozklad a v podstatě explicitní sestavení Mooreovy–Penroseovy pseudoinverze. Pokud ${\displaystyle r=\mathrm {rank} ({\mathbf {A}})}$, a její ekonomický singulární rozklad je

${\displaystyle {\mathbf {A}}={\mathbf {U}}_{r}{\mathbf {S}}_{r}{\mathbf {V}}_{r}^{T},\qquad {\text{pak}}\qquad {\mathbf {A}}^{\dagger }={\mathbf {V}}_{r}{\mathbf {S}}_{r}^{-1}{\mathbf {U}}_{r}^{T}}$

což umožňuje přímo nalézt řešení ve smyslu nejmenších čtverců minimální v normě.

Výpočet je použitelný pouze pro malé úlohy vzhledem k velké výpočetní náročnosti singulárního rozkladu.

Iterační metody

Pro řešení rozsáhlých úloh jsou standardem a jediným prakticky použitelným řešením iterační metody, zpravidla postavené na Krylovových podprostorech rostoucí dimenze. Klasickým představitelem je LSQR^[5][6] a další odvozené algoritmy CGLS, CGNE.

Aplikace: Regresní analýza

Metoda nejmenších čtverců bývá často používána při regresní analýze pro aproximaci zadaných (naměřených) hodnot nějakou funkcí z předepsaného prostoru. Nejjednodušším příkladem je proložení (aproximace) dat přímkou, tedy lineární funkcí. Protože klasická metoda nejmenších čtverců vede vždy na lineární aproximační model (de-facto soustavu rovnic) je často považována za ekvivalent pojmu lineární regrese. To souvisí s faktem, že libovolný aproximační problém ${\displaystyle {\mathbf {A}}{\mathbf {x}}\approx {\mathbf {b}}}$ lze interpretovat jako lineární regresi v ${\displaystyle m}$-rozměrném prostoru, kde jsme v bodě o souřadnicích ${\displaystyle (a_{j,1},\ldots ,a_{j,m})}$ naměřili nějakou veličinu ${\displaystyle b_{j}}$, ${\displaystyle j=1,\ldots ,n}$ a naměřené hodnoty prokládáme nadrovinou.

Pro první přiblížení uvažujme závislost nějaké nezávisle proměnné (např. fyzikální veličiny) ${\displaystyle y}$ na nezávisle proměnné ${\displaystyle u}$, tj. ${\displaystyle y=f(u)}$. přičemž závislost má nějaký předem daný tvar, např. ${\displaystyle f(u)=k\sin(u)+q\exp(-u)}$, kde koeficienty ${\displaystyle k}$ a ${\displaystyle q}$ jsou známé. Pro identifikaci těchto koeficientů provedeme ${\displaystyle n}$ měření veličiny ${\displaystyle y}$ v přesně definovaných hodnotách nezávisle proměnné ${\displaystyle u}$. Získáme tak sadu ${\displaystyle n}$ dvojic ${\displaystyle (u_{j},y_{j})}$ přičemž hodnoty ${\displaystyle y_{j}}$ jsou zatížené chybami měření. Dostaneme tak lineární aproximační problém

${\displaystyle {\mathbf {A}}{\mathbf {x}}=\left[{\begin{array}{cc}\sin(u_{1})&\exp(-u_{1})\\\vdots &\vdots \\\sin(u_{n})&\exp(-u_{n})\end{array}}\right]\left[{\begin{array}{c}k\\q\end{array}}\right]\approx \left[{\begin{array}{c}y_{1}\\\vdots \\y_{n}\end{array}}\right]={\mathbf {b}}.}$

Metoda nejmenších čtverců hledá takové hodnoty koeficientů ${\displaystyle k}$, ${\displaystyle q}$, aby součet čtverců „odchylek“ (reziduí) jejích funkčních hodnot od daných naměřených hodnot byl nejmenší možný.

Aproximace přímkou

Pro proložení daných hodnot přímkou (lineární funkcí, polynomem prvního řádu) s rovnicí ${\displaystyle y=f(u)=k_{1}u+k_{0}}$ dostaneme z normální soustavy rovnic vztahy

${\displaystyle k_{1}={\frac {n\sum {u_{i}y_{i}}-\sum {u_{i}}\sum {y_{i}}}{n\sum {u_{i}^{2}}-\left(\sum {u_{i}}\right)^{2}}},\qquad k_{0}={\frac {\sum {u_{i}^{2}}\sum {y_{i}}-\sum {u_{i}}\sum {u_{i}y_{i}}}{n\sum {u_{i}^{2}}-\left(\sum {u_{i}}\right)^{2}}}.}$

Aproximace parabolou

Zadané hodnoty lze aproximovat parabolou (kvadratickou funkcí, polynomem druhého řádu) s rovnicí ${\displaystyle y=f(u)=k_{2}u^{2}+k_{1}u+k_{0}}$. Optimální parametry ${\displaystyle k_{i}}$ získáme opět řešením normální soustavy rovnic

${\displaystyle {\mathbf {A}}^{T}{\mathbf {A}}{\mathbf {x}}=\left[{\begin{array}{ccc}\sum {u_{i}^{4}}&\sum {u_{i}^{3}}&\sum {u_{i}^{2}}\\\sum {u_{i}^{3}}&\sum {u_{i}^{2}}&\sum {u_{i}}\\\sum {u_{i}^{2}}&\sum {u_{i}}&n\end{array}}\right]\left[{\begin{array}{c}k_{2}\\k_{1}\\k_{0}\end{array}}\right]=\left[{\begin{array}{c}\sum {y_{i}u_{i}^{2}}\\\sum {y_{i}u_{i}}\\\sum {y_{i}}\end{array}}\right]={\mathbf {A}}^{T}{\mathbf {b}}.}$

Proložení bodů parabolou je lineární regresí kvadratické funkce (kvadratického modelu), zejména ve starší literatuře se můžeme setkat i s pojmem kvadratická regrese.^[7]

Aproximace polynomem

Obdobně jako v případě paraboly, i při aproximaci polynomem ${\displaystyle y=p_{s}(u)=k_{s}u^{s}+\ldots +k_{1}u+k_{0}}$ přímým dosazením hodnot ${\displaystyle y_{i}}$, ${\displaystyle u_{i}}$ získáme soustavu rovnic ${\displaystyle y_{i}=P_{s}(u_{i})}$. V maticovém zápisu

${\displaystyle {\mathbf {A}}{\mathbf {x}}=\left[{\begin{matrix}u_{1}^{s}&\cdots &u_{1}&1\\\vdots &\ddots &\vdots &\vdots \\u_{n}^{s}&\cdots &u_{n}&1\end{matrix}}\right]\left[{\begin{matrix}k_{s}\\\vdots \\k_{1}\\k_{0}\end{matrix}}\right]\approx \left[{\begin{matrix}y_{1}\\\vdots \\y_{n}\end{matrix}}\right]={\mathbf {b}}.}$

Přejdeme-li čistě formálně k normální soustavě rovnic (při řešení reálných problémů tuto soustavu nikdy nesestavujeme), dostáváme

${\displaystyle {\mathbf {A}}^{T}{\mathbf {A}}{\mathbf {x}}=\left[{\begin{matrix}\sum {u_{i}^{2s}}&\cdots &\sum {u_{i}^{s+1}}&\sum {u_{i}^{s}}\\\vdots &\ddots &\vdots &\vdots \\\sum {u_{i}^{s+1}}&\cdots &\sum {u_{i}^{2}}&\sum {u_{i}}\\\sum {u_{i}^{s}}&\cdots &\sum {u_{i}}&n\end{matrix}}\right]\left[{\begin{matrix}k_{s}\\\vdots \\k_{1}\\k_{0}\end{matrix}}\right]=\left[{\begin{matrix}\sum {y_{i}u_{i}^{s}}\\\vdots \\\sum {y_{i}u_{i}}\\\sum {y_{i}}\end{matrix}}\right]={\mathbf {A}}^{T}{\mathbf {b}},}$

která má vždy řešení. Pokud má matice ${\displaystyle {\mathbf {A}}}$ lineárně nezávislé sloupce, pak ${\displaystyle (A^{T}A)}$ je regulární a ${\displaystyle {\mathbf {x}}=\left({\mathbf {A}}^{T}{\mathbf {A}}\right)^{-1}{\mathbf {A}}^{T}{\mathbf {b}}}$ je jednoznačným řešením původního problému ve smyslu nejmenších čtverců.

Proložení bodů polynomem (předem) daného stupně ${\displaystyle s}$ je lineární regresí polynomu (polynomiálního modelu), zejména ve starší literatuře se můžeme setkat i s pojmem polynomiální (polynomická) regrese.^[7]

Aplikace: Nalezení průsečíku několika nadrovin v prostoru

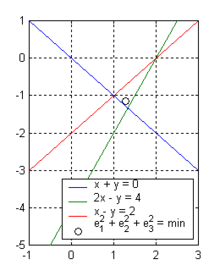
Opět se snažíme úlohu přeformulovat jako lineární aproximační problém ${\displaystyle {\mathbf {A}}{\mathbf {x}}\approx {\mathbf {b}}}$. Mechanismus lze nejsnáze ilustrovat na příkladu nalezení průsečíku několika přímek v rovině. Jsou dány tři přímky v rovině

${\displaystyle u+v=0,\quad 2u-v-4=0,\quad u-y-2=0,}$

které nemají společný průsečík. Zřejmě

${\displaystyle {\mathbf {A}}{\mathbf {x}}=\left[{\begin{matrix}1&1\\2&-1\\1&-1\end{matrix}}\right]\left[{\begin{matrix}u\\v\end{matrix}}\right]\approx \left[{\begin{matrix}0\\4\\2\end{matrix}}\right]={\mathbf {b}}}$

a vektor ${\displaystyle {\mathbf {e}}={\mathbf {A}}{\mathbf {x}}-{\mathbf {b}}}$ je nenulový pro libovolné ${\displaystyle u}$ a ${\displaystyle v}$. Za předpokladu, že přímky nejsou známy přesně (jejich popis je zatížen chybami) a chyby jsou obsaženy pouze v konstantních členech (tedy v pravé straně ${\displaystyle {\mathbf {b}}}$ aproximačního problému), můžeme použít k nalezení nejpravděpodobnějšího místa průsečíku metodu nejmenších čtverců. Získáme tak bod

${\displaystyle {\mathbf {x}}=\left({\mathbf {A}}^{T}{\mathbf {A}}\right)^{-1}{\mathbf {A}}^{T}{\mathbf {b}}\doteq \left[{\begin{matrix}1.286\\-1.143\end{matrix}}\right].}$

Všimněme si, že při přenásobení kterékoliv z rovnic definujících přímky nenulovou konstantou (různou od ${\displaystyle \pm 1}$), pracujeme se stejnými přímkami ale hledaný bod vyjde jinde. Taková operace totiž není v problému nejmenších čtverců ekvivalentní operací, fakticky taková operace změní normu, ve které provádíme minimalizaci.

Odkazy

Reference

Související články

• Lineární regrese
• Kvadratická regrese
• Polynomická regrese
• Exponenciální regrese
• Ortogonální regrese, error-in-variables modelling (EIV), úplný problém nejmenších čtverců (TLS)
• Regresní analýza
• Singular value decomposition (SVD), singulární rozklad

Externí odkazy

• Obrázky, zvuky či videa k tématu metoda nejmenších čtverců na Wikimedia Commons
• Encyklopedické heslo Čtverec v Ottově slovníku naučném ve Wikizdrojích
• http://herodes.feld.cvut.cz/… – aproximace přímkou, exponenciálou (linearizace) a polynomem
• http://amper.ped.muni.cz/… – aproximace obecnou funkcí, přímkou, polynomem, statistika
• http://cmp.felk.cvut.cz/… – aproximace polynomem, soustava s obdélníkovou maticí
• http://www.vscht.cz/kot/era/… Archivováno 29. 9. 2007 na Wayback Machine. – program ERA (autor Doc. Zámostný VŠCHT)