Spojité zobrazení

Spojité zobrazení je pojem z topologie a matematické analýzy. Je to takové zobrazení, které zobrazuje dostatečně blízké body blízko sebe. Tato vlastnost zobrazení se nazývá spojitost. Spojité zobrazení je zobecněním pojmu spojitá funkce na množinách čísel.

Neformální úvod

Spojitost je přirozená a očekávatelná vlastnost zobrazení. Pro reálné funkce spojitost znamená, že graf funkce neobsahuje ostré skoky a vypadá jako souvislá křivka. Pojem lze definovat na metrických prostorech, tedy na množinách, na kterých je možné měřit "vzdálenosti". Jedná se tedy například o množiny bodů v rovině, anebo také nějakou množinu funkcí. V metrických prostorech spojitost znamená, že pokud se nějaký bod blíží jinému bodu, blíží se k sobě i obrazy.

Metrickou definici lze zobecnit na topologické prostory, tj. na ještě širší skupinu množin, než jsou metrické prostory. V topologii je spojitost definována tak, že množiny zachovávají některé své topologické vlastnosti. Spojité zobrazení například převádí souvislé množiny na souvislé, kompaktní na kompaktní a vzor otevřené množiny je otevřená množina. Tyto různé definice spojitosti jsou vzájemně kompatibilní.

Formální definice

V topologických prostorech

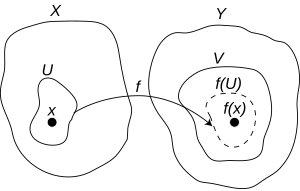
Zobrazení ${\displaystyle f}$ mezi topologickými prostory ${\displaystyle X}$ a ${\displaystyle Y}$ nazveme spojité, pokud vzor každé otevřené množiny v ${\displaystyle Y}$ je otevřená množina v ${\displaystyle X}$.

Ekvivalentní definice říká, že zobrazení ${\displaystyle f}$ je spojité v bodě ${\displaystyle x\in X}$, jestliže pro každé okolí ${\displaystyle V}$ bodu ${\displaystyle f(x)}$ existuje okolí ${\displaystyle U}$ bodu ${\displaystyle x}$ takové, že ${\displaystyle f(U)\subseteq V}$. Zobrazení ${\displaystyle f}$ je spojité, pokud je ${\displaystyle f}$ spojité v každém ${\displaystyle x\in X}$.

V metrických prostorech

Zobrazení ${\displaystyle f}$ z metrického prostoru prostoru ${\displaystyle (X,\rho )\,\!}$ do ${\displaystyle (Y,\sigma )\,\!}$ je spojité, právě když pro každé ${\displaystyle x_{0}\in X\,\!}$ a kladné reálné číslo ${\displaystyle \epsilon \,\!}$ existuje kladné reálné ${\displaystyle \delta \,\!}$ takové, že pro každý bod ${\displaystyle x\in X\,\!}$ splňující ${\displaystyle \rho (x,x_{0})<\delta \,\!}$ platí ${\displaystyle \sigma (f(x_{0}),f(x))<\epsilon \,\!}$. Jinými slovy, vzdálenost obrazů dvou bodů může být libovolně blízká, pokud zvolíme vzdálenost vzorů dostatečně blízko.

Ekvivalentně, zobrazení ${\displaystyle f:\,X\to Y}$ je spojité v bodě ${\displaystyle x\in X\,\!}$, jestliže platí implikace

${\displaystyle x_{n}\to x\Rightarrow f(x_{n})\to f(x)\,}$.

Spojitá zobrazení na množinách čísel

Zobrazením mezi množinami čísel se častěji říká funkce. Funkce f je spojitá v bodě x, pokud pro každé ${\displaystyle \epsilon >0}$ existuje ${\displaystyle \delta >0\,\!}$ takové, že ${\displaystyle |x-y|<\delta \,\!}$ implikuje ${\displaystyle |f(x)-f(y)|<\epsilon \,\!}$.

Množina reálných a komplexních čísel je však také topologický prostor, generován otevřenými intervaly. Podobně metrický prostor a normovaný lineární prostor jsou topologické prostory a různé definice spojitosti zobrazení mezi těmito prostory jsou ekvivalentní.

Vlastnosti spojitých zobrazení

• Složení spojitých zobrazení je opět spojité zobrazení.
• Spojité zobrazení zachovává kompaktní množiny. Proto i složení ${\displaystyle f\circ g:X\rightarrow Z}$ spojitého zobrazení ${\displaystyle f:Y\rightarrow Z}$ s kompaktním zobrazením ${\displaystyle g:X\rightarrow Y}$ je zobrazení kompaktní.

Příklady spojitých a nespojitých zobrazení

• Sčítání, odčítání, násobení a dělení čísel jsou spojitá zobrazení (z "dvojic" čísel do čísel).
• Mapa zobrazující část krajiny se dá chápat jako spojité zobrazení. Tento koncept je formalizován v definici variety. Varieta je zadána pomocí atlasu, který pozůstává ze spojitých map.
• Projekce topologického vektorového prostoru na nějaký podprostor je spojité zobrazení.
• Lineární transformace konečně rozměrného vektorového prostoru je spojitá.
• Polynomiální funkce je spojité zobrazení. Podobně zobrazení z ${\displaystyle \mathbb {R} ^{n}}$ do ${\displaystyle \mathbb {R} ^{m}}$, kterého každá složka je polynomiální funkce.
• Křivka je spojité zobrazení z úsečky do nějakého topologického prostoru.
• Skalární součin je spojité zobrazení z dvojic vektorů do čísel.
• Funkce ${\displaystyle f:\mathbb {R} \to \{0,1\}}$, která racionálním číslům přiřadí nulu a iracionálním jednotku, je nespojitá.
• Evoluční operátor v kvantové fyzice (popisuje vývoj fyzikálního systému v čase) je spojité zobrazení.
• Násobení v Lieově grupě je spojité.
• Každé zobrazení z diskrétního prostoru do libovolného metrického prostoru je spojité ^{[pozn 1]}.
• Mějme X prostor spojitých reálných funkcí na intervalu ${\displaystyle \scriptstyle \left\langle 0,\,1\right\rangle }$ spolu se supremovou normou (||f||:=sup |f(x)|) a nechť K(x,t) je spojitá funkce. Definujme ${\displaystyle \scriptstyle A:\,X\to X,\ (Ax)(t)=\int _{0}^{1}K(t,\,s)x(s)ds}$. Pak ${\displaystyle \scriptstyle A\,}$ je spojité zobrazení v ${\displaystyle \scriptstyle \ C\left(\left\langle 0,\,1\right\rangle \right)}$.
• Příkladem spojitého zobrazení na topologickém prostoru, který není metrizovatelný, je funkce ${\displaystyle \aleph }$, která ordinálnímu číslu ${\displaystyle \alpha }$ přiřadí ${\displaystyle \alpha }$-tou nejmenší nekonečnou mohutnost. Jedná se o zobrazení na vlastní třídě, ovšem pro každé ordinální číslo ${\displaystyle \beta }$ (které je zároveň množinou ordinálních čísel) je restrikce této funkce na ${\displaystyle \beta }$ spojitým ^{[pozn 2]} zobrazením z ${\displaystyle \beta }$ do obrazu ${\displaystyle \aleph [\beta ]}$.
• Lineární zobrazení nekonečně rozměrného vektorového prostoru může, ale také nemusí být spojité. Nechť ${\displaystyle X=C^{\infty }(\langle 0,1\rangle )}$ je prostor hladkých funkcí spolu s maximovou normou ||f||=sup |f(x)|. Pak derivace ${\displaystyle D:X\to X}$ je lineární nespojité zobrazení. ^{[pozn 3]}.

Odkazy

Poznámky

Související články

• Spojitá funkce
• Topologie
• Homeomorfismus
• Omezený operátor
• Lineární zobrazení

Externí odkazy

• Obrázky, zvuky či videa k tématu spojitá funkce na Wikimedia Commons
• Téma Spojitost ve Wikicitátech