Exponentialverteilung

Die Exponentialverteilung (auch negative Exponentialverteilung) ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der nicht-negativen reellen Zahlen, die durch eine Exponentialfunktion gegeben ist. Sie wird als Modell vorrangig bei der Beantwortung der Frage nach der Länge von zufälligen Zeitintervallen benutzt, wie z. B.
- Zeit zwischen zwei Anrufen
- Lebensdauer von Atomen beim radioaktiven Zerfall
- Lebensdauer von Bauteilen, Maschinen und Geräten, wenn Alterungserscheinungen nicht betrachtet werden müssen.
- als grobes Modell für kleine und mittlere Schäden in Hausrat, Kraftfahrzeug-Haftpflicht, Kasko in der Versicherungsmathematik
steht für die Zahl der erwarteten Ereignisse pro Einheitsintervall. Wie aus dem Diagramm ersichtlich, sind kürzere Intervalle zwischen Ereignissen (Intervalllänge ) wahrscheinlicher. Seltener treten aber auch sehr lange Intervalle auf. Die Wahrscheinlichkeitsdichte kann durchaus Werte >1 annehmen (z. B. für ), da die Fläche unter der Kurve auf 1 normiert ist (Normierungseigenschaft). Konkrete Wahrscheinlichkeitsangaben über das Eintreten des nächsten Ereignisses gewinnt man hier am ehesten aus der Verteilungsfunktion.
Oft ist die tatsächliche Verteilung keine Exponentialverteilung, jedoch ist die Exponentialverteilung einfach zu handhaben und wird zur Vereinfachung unterstellt. Sie ist anwendbar, wenn ein Poisson-Prozess vorliegt, also die poissonschen Annahmen erfüllt sind.
Die Exponentialverteilung ist ein Teil der viel größeren und allgemeineren Exponentialfamilie, einer Klasse von Wahrscheinlichkeitsmaßen, die sich durch eine leichte Handhabbarkeit auszeichnen.
Definition
Eine stetige Zufallsvariable genügt der Exponentialverteilung mit dem positiven reellen inversen Skalenparameter , wenn sie die Dichtefunktion
besitzt. Wenn eine Zufallsvariable diese Dichte hat, dann schreibt man auch oder .
Der Parameter besitzt den Charakter einer Ereignisrate und den eines Ereignisabstandes (mittlere Reichweite oder mittlere Lebensdauer).
Eine (vor allem im angelsächsischen Raum übliche) alternative Parametrisierung führt zur Dichtefunktion
Die Beziehung zur obigen Parametrisierung ist dabei einfach . Um Missverständnissen vorzubeugen, wird empfohlen, den Erwartungswert explizit anzugeben, also von einer Exponentialverteilung mit Erwartungswert zu sprechen.
Eigenschaften
Verteilungsfunktion
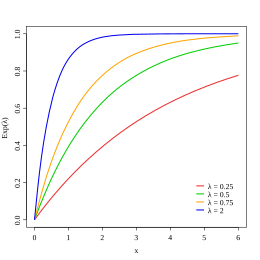
Die (kumulative) Verteilungsfunktion der Exponentialverteilung ist
Sie erlaubt die Berechnung der Wahrscheinlichkeit des Auftretens des nächsten Ereignisses im Intervall von bis .
Die Wahrscheinlichkeit für eine Intervalllänge größer als bis zum nächsten Ereignis beträgt .
Erwartungswert
Die Exponentialverteilung besitzt den Erwartungswert , denn
- .
Der Erwartungswert entspricht der mittleren Betriebsdauer von Bauteilen, Maschinen und Geräten, wenn Alterungserscheinungen nicht betrachtet werden müssen. Er wird in diesem Zusammenhang als Mean Time Between Failures (MTBF) bezeichnet.
Median
Die Exponentialverteilung besitzt ihren Median bei
- .
Modus
Den maximalen Wert nimmt die Dichtefunktion der Exponentialverteilung bei an, d. h., der Modus ist
- .
Varianz
Die Varianz ergibt sich analog mittels
- .
Standardabweichung
Für die Standardabweichung ergibt sich
- .
Variationskoeffizient
Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten. Es gilt
- .
Also gilt
- .
Geometrischer Mittelwert
Das Geometrische Mittel der Exponentialverteilung ist
- ,
wobei die Euler-Mascheroni-Konstante bezeichnet.
Weitere Streumaße
Die mittlere absolute Abweichung
ist kleiner als die Standardabweichung, die mittlere absolute Abweichung bezüglich des Medians
ist noch etwas kleiner.
Schiefe
Die Schiefe besitzt unabhängig vom Parameter immer den Wert 2. Die Verteilung ist ein typischer Vertreter einer rechtsschiefen Verteilung, für die auch gilt.
Wölbung
Die Wölbung besitzt unabhängig vom Parameter immer den Wert 9. Somit hat der Exzess den Wert 6.
Quantile
Die Quantilfunktion der Exponentialverteilung lässt sich angeben und ist
- .
Damit ist der Interquartilabstand .
Höhere Momente
Die k-ten Momente sind
- .
Dies lässt sich zum Beispiel mit der k-ten Ableitung der momenterzeugenden Funktion zeigen.
Kumulanten
Die kumulantenerzeugende Funktion ist
- für .
Damit ist die k-te Kumulante
Charakteristische Funktion
Die charakteristische Funktion hat die Form
- .
Momenterzeugende Funktion
Die momenterzeugende Funktion der Exponentialverteilung ist
- für .
Entropie
Die Entropie der Exponentialverteilung beträgt
- .
Überlebenswahrscheinlichkeit
Da die Exponentialverteilung auch als Lebensdauerverteilung und im technischen Bereichen als Ausdruck für die Zuverlässigkeit eines Gerätes verwendet wird, ist es möglich, damit zusammenhängende Größen wie Überlebensfunktion und die Ausfallrate mit Hilfe der Verteilungsfunktion anzugeben. So nennt man das Komplement der Verteilungsfunktion die Überlebensfunktion:
Damit ergibt sich unmittelbar die auf einen Zeitpunkt bezogene bedingte Überlebenswahrscheinlichkeit
Die Exponentialverteilung ist eine gedächtnislose Lebensdauerverteilung, d. h. die Überlebenswahrscheinlichkeit in Bezug auf einen bestimmten Zeitpunkt ist unabhängig vom bisher erreichten Alter. Im Gegensatz zur Weibull-Verteilung kann die Exponentialverteilung nur für sogenannte ermüdungsfreie Systeme verwendet werden
Die Ausfallrate ergibt sich zu
Sie ist für die Exponentialverteilung zeitlich und räumlich konstant und wird in der Literatur üblicherweise mit der Konstanten λ bezeichnet.
Gedächtnislosigkeit
Die Exponentialverteilung ist im folgenden Sinne gedächtnislos: Ist bekannt, dass eine exponentialverteilte Zufallsvariable den Wert überschreitet, so ist die bedingte Wahrscheinlichkeit, dass sie um mindestens überschreitet, genau so groß wie die, dass eine exponentialverteilte Zufallsvariable (mit gleichem Parameter ) den Wert überschreitet, formal
- .
Die Gedächtnislosigkeit ist sogar eine definierende Eigenschaft der Exponentialverteilung; diese ist die einzig mögliche stetige Verteilung mit dieser Eigenschaft. Dies folgt direkt mit der Definition der bedingten Wahrscheinlichkeit und der daraus entstehenden Funktionalgleichung. Das diskrete Pendant hierzu ist die geometrische Verteilung als einzig mögliche diskrete gedächtnislose Verteilung.
Die Exponentialverteilung ist folglich auch die einzige stetige Wahrscheinlichkeitsverteilung, die eine konstante Ausfallrate aufweist.
Weitere Eigenschaften
Sind stochastisch unabhängig, so ist
Sind stochastisch unabhängig, so die Summe ist Erlang-verteilt.
Beziehung zu anderen Verteilungen
Beziehung zur stetigen Gleichverteilung
Wenn eine auf dem Intervall gleichverteilte stetige Zufallsvariable ist, dann genügt der Exponentialverteilung mit dem Parameter .
Beziehung zur Normalverteilung
Sind die Zufallsvariablen und standardnormalverteilt und unabhängig, so ist exponentialverteilt mit Parameter .
Beziehung zur geometrischen Verteilung
In Analogie zur diskreten geometrischen Verteilung bestimmt die stetige Exponentialverteilung die Wartezeit bis zum ersten Eintreffen eines Ereignisses, das gemäß einem Poisson-Prozess auftritt; die geometrische Verteilung kann also als diskretes Äquivalent zur Exponentialverteilung betrachtet werden.
- Wenn , dann ist , eine geometrische Verteilung auf .
- Wenn , dann ist , eine geometrische Verteilung auf .
Beziehung zur Gammaverteilung
- Die Verallgemeinerung der Exponentialverteilung, d. h. die Wartezeit bis zum Eintreffen des -ten Ereignisses eines Poisson-Prozesses, wird mit der Gammaverteilung beschrieben. Die Exponentialverteilung mit Parameter ist also identisch mit der Gammaverteilung mit Parametern und . Die Exponentialverteilung besitzt demnach auch alle Eigenschaften der Gammaverteilung. Insbesondere ist die Summe von unabhängigen, -verteilten Zufallsvariablen gamma- oder Erlang-verteilt mit Parametern und .
- Die Faltung von zwei Exponentialverteilungen mit demselben ergibt eine Gammaverteilung mit , .
Beziehung zur Gamma-Gamma-Verteilung
Ist der Parameter der Exponentialverteilung eine Zufallsvariable, die wie eine Gammaverteilung verteilt ist, dann ist die hervorgehende Zufallsvariable wie eine Gamma-Gamma-Verteilung verteilt.
Beziehung zur Pareto-Verteilung
Wenn Pareto-verteilt mit Parametern und ist, dann ist exponentialverteilt mit dem Parameter .
Beziehung zur Poisson-Verteilung
Die Abstände zwischen dem Eintreten zufälliger Ereignisse können häufig mit der Exponentialverteilung beschrieben werden. Insbesondere gilt, dass der Abstand zwischen zwei aufeinanderfolgenden Ereignissen eines Poisson-Prozesses mit Rate exponentialverteilt mit dem Parameter ist. In diesem Fall ist die Anzahl der Ereignisse in einem Intervall der Länge Poisson-verteilt mit Parameter .
Herleitung: Sei w eine Orts- oder Zeitvariable und die kleine konstante Eintretenshäufigkeit von Ereignissen im Einheitsintervall von w. Dann findet man mit den poissonschen Annahmen die Wahrscheinlichkeit für das nächste Eintreten eines Ereignisses im kleinen Intervall als Produkt der Wahrscheinlichkeit, kein Ereignis bis w und eins im Intervall zu haben:
Daraus ergibt sich nach Division durch die Wahrscheinlichkeitsdichte der Exponentialverteilung mit als Ereignisrate und als mittlerem Ereignisabstand.
Beziehung zur Erlang-Verteilung
- Für einen Poisson-Prozess wird die zufällige Anzahl der Ereignisse bis zu einem definierten Zeitpunkt mittels Poisson-Verteilung bestimmt, die zufällige Zeit bis zum -ten Ereignis ist Erlang-verteilt. Im Fall geht diese Erlang-Verteilung in eine Exponentialverteilung über , mit der die Zeit bis zum ersten zufälligen Ereignis sowie die Zeit zwischen zwei aufeinanderfolgenden Ereignissen bestimmt werden kann.
- Die Summe von unabhängigen exponentialverteilten Zufallsgrößen hat die Erlang-Verteilung -ter Ordnung .
Beziehung zur Weibull-Verteilung
- Mit geht die Weibull-Verteilung in die Exponentialverteilung über. Mit anderen Worten: Die Exponentialverteilung behandelt Probleme mit konstanter Ausfallrate . Untersucht man jedoch Fragestellungen mit steigender () oder fallender () Ausfallrate, dann geht man von der Exponentialverteilung zur Weibull-Verteilung über.
- Wenn exponentialverteilt ist, dann ist Weibull-verteilt.
Beziehung zur Chi-Quadrat-Verteilung
Die Chi-Quadrat-Verteilung geht für in die Exponentialverteilung mit dem Parameter über.
Beziehung zur Rayleigh-Verteilung
Wenn exponentialverteilt ist mit Rate , dann ist Rayleigh-verteilt mit Skalenparameter .
Beziehung zur Laplace-Verteilung
Sind zwei unabhängige Zufallsvariablen, die beide Exponentialverteilt zum Parameter sind, dann ist sowohl als auch Laplace-verteilt.
Beziehung zur Standard-Gumbel-Minimum-Verteilung
Die Dichte des Logarithmus einer standard-exponentialverteilten Zufallsvariablen folgt einer Standard-Gumbel-Verteilung (Minimum)
- .
Anwendungsbeispiel
Die Exponentialverteilung ist eine typische Lebensdauerverteilung. So ist beispielsweise die Lebensdauer von elektronischen Bauelementen häufig annähernd exponentialverteilt. Hierbei spielt besonders die Gedächtnislosigkeit eine bedeutende Rolle: die Wahrscheinlichkeit, dass ein x Tage altes Bauelement noch mindestens t Tage hält, ist demnach genauso groß wie die, dass ein neues Bauelement überhaupt t Tage hält. Charakteristisch bei der Exponentialverteilung ist die konstante Ausfallrate .
Dies ist zum Beispiel bei Glühlampen nur annähernd richtig, da diese nur beim Einschalten stark beansprucht werden. Auf Lebewesen darf ebenfalls keine Exponentialverteilung angewendet werden, sonst wäre zum Beispiel die Wahrscheinlichkeit, dass ein Achtzigjähriger noch weitere fünfzig Jahre lebt, genauso hoch wie die, dass ein Neugeborener das fünfzigste Lebensjahr erreicht.
Beispiel: In einer Elektronikfirma werden Funkwecker produziert. Im Rahmen der Qualitätssicherung wird anhand von Reklamationen die Funktionsdauer der Wecker untersucht. Es stellt sich heraus, dass durchschnittlich pro Tag 5 ‰ der Wecker unabhängig von ihrem Alter ausfallen.
Die Zufallsgröße „Zeitdauer der Funktionsfähigkeit eines Funkweckers in Tagen“ ist also exponentialverteilt mit der Ausfallrate . Entsprechend beträgt die durchschnittliche Zeitdauer, bis ein Wecker ausfällt, Tage.
Die Wahrscheinlichkeit, dass ein Wecker höchstens (noch) 20 Tage hält, ist
d. h. nach 20 Tagen sind durchschnittlich ca. 10 % der Wecker ausgefallen.
Entsprechend ist der Anteil der Wecker, die mindestens 180 Tage aushalten,
also halten durchschnittlich ca. 40 % der Wecker länger als 180 Tage.
Obwohl bei einer exponentialverteilten Lebensdauerverteilung am Anfang absolut betrachtet mehr Geräte ausfallen, ist die Ausfallrate konstant: in jedem Zeitintervall fallen relativ betrachtet immer gleich viele Geräte aus. Dieser Umstand darf nicht mit den Frühausfällen der Badewannenkurve verwechselt werden. Hier ist zu Beginn die Ausfallrate höher und nicht konstant über die Lebensdauer. Zur Beschreibung der Badewannenkurve ist eine andere Lebensdauerverteilung (Weibull-Verteilung) notwendig.
Zufallszahlen
Zur Erzeugung exponentialverteilter Zufallszahlen bietet sich die Inversionsmethode an.
Die nach dem Simulationslemma zu bildende Inverse der Verteilungsfunktion lautet hierbei . Zu einer Folge von Standardzufallszahlen lässt sich daher eine Folge exponentialverteilter Zufallszahlen berechnen. Einfacher kann stattdessen auch gerechnet werden.
Siehe auch
- Mortalität (Übergang von der Exponentialverteilung zur Weibull-Verteilung)
- Liste univariater Wahrscheinlichkeitsverteilungen
- Doppelexponentialverteilung
Weblinks
- www.exponentialverteilung.de – Erklärung, Aufgaben, Veranschaulichung

















































![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


















![{\displaystyle [w,w+\Delta w]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27b2040fcb6fda995a889b38b998fc103ffa422e)




































