Konfidenzintervall für die Erfolgswahrscheinlichkeit der Binomialverteilung

Ein Konfidenzintervall für die Erfolgswahrscheinlichkeit der Binomialverteilung ist ein Konfidenzintervall (Vertrauensbereich) für den unbekannten Parameter ${\displaystyle p}$ der Binomialverteilung (nach Beobachtung von ${\displaystyle k}$ Treffern in einer Stichprobe der Größe ${\displaystyle n}$).

Exakte Konfidenzintervalle erhält man unter Zuhilfenahme der Binomialverteilung. Es gibt aber auch Näherungsmethoden, die (meistens) auf der Approximation der Binomialverteilung durch die Normalverteilung basieren.^[1]

Einführendes Beispiel

Um den unbekannten relativen Anteil ${\displaystyle p}$ einer politischen Partei A in der Wählerschaft zu schätzen, werden in einer Meinungsumfrage ${\displaystyle n=400}$ Personen befragt, ob sie die Partei A wählen werden. Das exakte Vorgehen ist: Wir wählen 400 Mal eine zufällige Person aus der Wählerschaft aus und befragen diese. Dabei halten wir nicht fest, ob diese Person schon einmal befragt wurde. Es kann also vorkommen, wenngleich es auch bei einer großen Wählerschaft entsprechend unwahrscheinlich ist, dass dieselbe Person mehrmals befragt wird. Die Anzahl ${\displaystyle X}$ der Befragten, die angeben, die Partei A zu wählen, ist vom Zufall abhängig und deshalb eine Zufallsvariable. Da die befragten Personen zufällig und unabhängig voneinander ausgewählt werden, ist die Zufallsvariable ${\displaystyle X}$ binomialverteilt mit den Parametern ${\displaystyle n=400}$ und dem unbekannten Parameter ${\displaystyle p}$. Nehmen wir an, in der Umfrage haben ${\displaystyle k=20}$ Befragte angegeben, die Partei A zu wählen. Man berechnet einen Schätzwert ${\displaystyle {\hat {p}}}$ von ${\displaystyle p}$ als:

${\displaystyle {\hat {p}}={\frac {k}{n}}=0{,}05\,}$.

Man nennt dies eine Punktschätzung, weil nur ein Wert als Schätzung von ${\displaystyle p}$ berechnet wird.

Der wahre Wert des relativen Anteils ${\displaystyle p}$ kann sowohl kleiner als auch größer als der Punktschätzwert ${\displaystyle {\hat {p}}}$ sein. Mit Sicherheit gilt nur, dass ${\displaystyle p}$ jeden Wert zwischen 0 und 1 annehmen kann. Wünschenswert wäre ein Konfidenzintervall ${\displaystyle [p_{u},p_{o}]}$ für ${\displaystyle p}$. Beim vielfachen Wiederholen des Verfahrens sollen die berechneten Konfidenzintervalle in den „meisten Fällen“ den Parameter ${\displaystyle p}$ enthalten. Wie oft das der Fall sein soll, wird mittels der Vertrauenswahrscheinlichkeit (oder auch Konfidenzniveau) ${\displaystyle \gamma }$ ausgedrückt. Das berechnete Intervall ${\displaystyle [p_{u},p_{o}]}$ wird Konfidenzintervall (oder Vertrauensbereich) genannt. Oft wird ${\displaystyle \gamma }$ gleich 95 % gewählt. Das bedeutet, dass bei Wiederholung des Verfahrens für 95 % aller Stichproben die Aussage ${\displaystyle p\in [p_{u},p_{o}]}$ richtig ist.

Wald-Intervall: Einfache Approximation durch die Normalverteilung

Gegeben sei die binomialverteilte Zahl der Erfolge ${\displaystyle X\sim B(X=k|p,n)}$, deren Mittelwert ${\displaystyle E(X)=pn}$ und Varianz ${\displaystyle \operatorname {Var} (X)=np(1-p)}$ sind. Bei der Schätzung des Parameters ${\displaystyle p=E(X)/n}$ ersetzt man den Erwartungswert durch die Zahl der Erfolge in der Stichprobe (der Größe n):

${\displaystyle {\hat {p}}=X/n}$.

Entsprechend folgt der Standardfehler

${\displaystyle \operatorname {SE} ({\hat {p}})={\sqrt {\operatorname {Var} ({\hat {p}})}}={\sqrt {\frac {\operatorname {Var} (X)}{n^{2}}}}={\frac {\sqrt {np(1-p)}}{n}}\approx {\frac {\sqrt {n{\hat {p}}(1-{\hat {p}})}}{n}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}.}$

Systematisch kann dieses Ergebnis auch durch den Standardfehlers des Maximum-Likelihood-Schätzers

${\displaystyle \operatorname {SE} ({\hat {p}})={\frac {1}{\sqrt {-{\frac {\partial ^{2}}{\partial \theta ^{2}}}\ell ({\hat {p}})}}}}$

erhalten werden, wobei ${\displaystyle \ell }$ die Loglikelihood-Funktion ist, siehe Konstruktion des Wald-Konfidenzintervalls^[2].

Daraus folgt die oft verwendete folgende Näherungsformel für die Grenzen des Konfidenzintervalls ${\displaystyle [p_{u},p_{o}]}$ (welches auch als Standard-Intervall oder Wald-Intervall bezeichnet wird):^[3]

${\displaystyle p_{u}={\hat {p}}-c\cdot {\sqrt {\frac {{\hat {p}}\cdot (1-{\hat {p}})}{n}}}}$

${\displaystyle p_{o}={\hat {p}}+c\cdot {\sqrt {\frac {{\hat {p}}\cdot (1-{\hat {p}})}{n}}}}$,

wobei ${\displaystyle c}$ eine Konstante ist, die vom Irrtumsniveau abhängt:

${\displaystyle c=\Phi ^{-1}\left(1-{\frac {\alpha }{2}}\right)}$,

wobei ${\displaystyle \alpha =1-\gamma }$ das Irrtumsniveau und ${\displaystyle \Phi ^{-1}}$ die Quantilfunktion der Standardnormalverteilung, also die Umkehrfunktion ihrer Verteilungsfunktion ${\displaystyle \Phi }$ bezeichnet (z. B. ${\displaystyle c\approx 1{,}96}$ für ${\displaystyle \alpha =0{,}05}$).

Wenn diese Formel verwendet wird, sollte ${\displaystyle k\geq 50}$ und ${\displaystyle n-k\geq 50}$ sein. Trotzdem kann die Verwendung des Standard-Intervalls problematisch sein. In der Abbildung ist als Beispiel die Überdeckungswahrscheinlichkeit für ${\displaystyle n=400}$ und ${\displaystyle p\in [0{,}125;0{,}875]}$ illustriert. Sie liegt oft unter dem geforderten Niveau von 0,95.

Ein weiterer großer Nachteil der Approximation ist, dass das untere Ende des Konfidenzintervalls für sehr kleine Erfolgswahrscheinlichkeiten empirisch nicht mögliche negative Werte überdecken kann bzw. bei sehr hohen Erfolgswahrscheinlichkeiten über 1 hinaus gehen kann.

Agresti-Coull-Intervall

Für dieses Intervall setzt man ${\displaystyle {\tilde {k}}=k+{\tfrac {c^{2}}{2}}}$, ${\displaystyle {\tilde {n}}=n+c^{2}}$, ${\displaystyle {\tilde {p}}={\tfrac {\tilde {k}}{\tilde {n}}}}$ und verwendet die (oben beschriebene) einfache Approximation mit diesen Parametern:

${\displaystyle p_{o,u}={\tilde {p}}\pm c\cdot {\sqrt {\frac {{\tilde {p}}\cdot (1-{\tilde {p}})}{\tilde {n}}}}}$

Der Mittelpunkt des Intervalls ist identisch zu dem des Wilson-Intervalls und das Intervall ist nie kürzer als ein Wilson-Intervall.^[4]

Falls γ = 0,95, dann ist ${\displaystyle c=1{,}96\approx 2}$ und man bekommt eine einfache Regel: ${\displaystyle {\tilde {k}}=k+2}$, ${\displaystyle {\tilde {n}}=n+4}$ und ${\displaystyle {\tilde {p}}={\tfrac {k+2}{n+4}}}$.

Wilson-Intervall

Dieses Intervall wurde 1927 von Edwin Bidwell Wilson vorgeschlagen und ist genauer als die einfache Approximation durch die Normalverteilung. Es gilt, mit dem gleichen ${\displaystyle c}$ wie im Abschnitt über die Approximation durch die Normalverteilung,

${\displaystyle p_{o,u}={\frac {1}{1+{\frac {c^{2}}{n}}}}\cdot \left({\hat {p}}+{\frac {c^{2}}{2n}}\pm c\cdot {\sqrt {{\frac {{\hat {p}}\cdot (1-{\hat {p}})}{n}}+{\frac {c^{2}}{4n^{2}}}}}\,\right)}$

Offenbar konvergieren die Intervallgrenzen für große ${\displaystyle n}$ gegen die Grenzen des Standard-Intervalls (da ${\displaystyle c^{2}/2n}$ und ${\displaystyle c^{2}/4n^{2}}$ mit wachsendem ${\displaystyle n}$ gegen Null gehen).

Durch Umformen erhält man die bei Brown/Cai/DasGupta auf Seite 107 angegebene Formel (4):

${\displaystyle p_{o,u}={\frac {k+{\frac {c^{2}}{2}}}{n+c^{2}}}\pm {\frac {c{\sqrt {n}}}{n+c^{2}}}\cdot {\sqrt {{\frac {k}{n}}\left(1-{\frac {k}{n}}\right)+{\frac {c^{2}}{4n}}}}}$

Die bei Henze auf Seite 228 angegebene Formel unterscheidet sich davon noch durch eine Stetigkeitskorrektur (von +0,5 oder −0,5 angewandt auf ${\displaystyle k}$).

Clopper-Pearson-Intervall

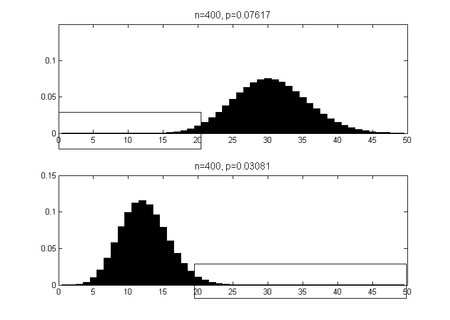
Von C. Clopper und Egon Pearson (1934) stammt das folgende exakte Verfahren, um die untere Grenze ${\displaystyle p_{u}}$ und die obere Grenze ${\displaystyle p_{o}}$ zu bestimmen.^[5] Es sei, wie bisher, ${\displaystyle n}$ die Größe der Stichprobe, ${\displaystyle k}$ die Anzahl der Erfolge und das Konfidenzniveau sei 95 %.

Die obere Grenze bestimmt man aus ${\displaystyle P(X\leq k;p_{o})=0{,}025}$ und die untere Grenze aus ${\displaystyle P(X\geq k;p_{u})=0{,}025}$, siehe Abbildung. Die untere Grenze lässt sich für ${\displaystyle k=0}$ mit dieser Formel nicht angeben.

Erläuterung: Wenn die Wahrscheinlichkeit, höchstens ${\displaystyle k}$ Erfolge zu erzielen, für einen Anteilswert ${\displaystyle p}$ die Grenze 0,025 unterschreitet, so kann bei einer Irrtumswahrscheinlichkeit von maximal 2,5 % ausgeschlossen werden, dass ${\displaystyle p}$ der gesuchte Anteilswert ist. Somit ist p_o der größte Wert von ${\displaystyle p}$, bei dem beim gegebenen Konfidenzniveau noch angenommen werden kann, dass k oder weniger Erfolge auftreten. Für größere Werte von ${\displaystyle p}$ erscheint dies zu unwahrscheinlich.

Für die untere Grenze gilt entsprechend: ${\displaystyle p_{u}}$ ist der kleinste Wert von ${\displaystyle p}$, bei dem noch angenommen wird, dass ${\displaystyle k}$ oder mehr Erfolge auftreten können. Für kleinere Werte von ${\displaystyle p}$ erscheint dies zu unwahrscheinlich, wobei auch hier die Irrtumswahrscheinlichkeit maximal 2,5 % beträgt. Somit liegt man in mindestens 95 % aller Fälle mit der Aussage „${\displaystyle p\leq p_{o}}$ und ${\displaystyle p\geq p_{u}}$“ richtig.

Praktische Berechnung

Die beiden Werte p_u, p_o lassen sich mit der verallgemeinerten inversen Verteilungsfunktion der Betaverteilung berechnen; dafür eignet sich beispielsweise die Funktion BETAINV^[6] gängiger Tabellenkalkulationsprogramme wie Excel oder LibreOffice Calc, in Python kann die Funktion scipy.stats.beta.ppf^[7] benutzt werden. Die Funktion gibt das Quantil der angegebenen Betaverteilung zurück und man erhält aufgrund des Zusammenhangs der Binomial- und Betaverteilung für die Auflösung der Gleichung ${\displaystyle P_{p}(X\leq k)=\alpha }$:

${\displaystyle p=\operatorname {BETAINV} (1-\alpha /2;k+1;n-k)}$. Im Folgenden bezeichnen wir wie bisher das Konfidenzniveau mit ${\displaystyle \gamma }$, außerdem sei ${\displaystyle \alpha =1-\gamma }$.

Im Beispiel mit ${\displaystyle n=400,k=20}$ sowie Konfidenzniveau von 95 % erhält man so für die untere Grenze des Konfidenzintervalls:

P(X ≥ 20) = 0,025

P(X ≤ 19) = 0,975

${\displaystyle p_{u}=\operatorname {BETAINV} (1-0{,}975;20;400-19)=0{,}03081}$

und für die obere Grenze des Konfidenzintervalls:

${\displaystyle P(X\leq 20)=0{,}025}$

${\displaystyle p_{o}=\operatorname {BETAINV} (1-0{,}025;21;400-20)=0{,}07617}$

Die Berechnung der Grenzen des Konfidenzintervalls mit scipy.stats.beta.ppf erfolgt analog:

from scipy.stats import beta
k = 20
n = 400
alpha = 0.05
p_u, p_o = beta.ppf([alpha/2, 1 - alpha/2], [k, k + 1], [n - k + 1, n - k])

Erläuterung des Ergebnisses in Worten: In der Stichprobe von 400 befragten Personen gaben 20 Personen an, Partei A zu wählen. Damit lässt sich bei 95-prozentiger Konfidenz der Stimmanteil der Partei A in der gesamten Bevölkerung mit 3,1 % – 7,6 % abschätzen.

Die Methode ist in der folgenden Tabelle zusammengefasst:

Analyse der Überdeckungswahrscheinlichkeit

Ist ${\displaystyle C(k)}$ das Konfidenzintervall zu ${\displaystyle k}$ Erfolgen, so verlangt man laut Definition, dass für alle ${\displaystyle p}$ die Überdeckungswahrscheinlichkeit ${\displaystyle P_{p}(k\in \{0,\ldots ,n\}:p\in C(k))}$ größer oder gleich ${\displaystyle \gamma }$; ist. Bei stetigen Verteilungen lassen sich Konfidenzintervalle finden, so dass hier Gleichheit vorliegt (also ${\displaystyle =\gamma }$ statt ${\displaystyle \geq \gamma }$). Dies ist für die diskrete Binomialverteilung nicht möglich. In folgender Abbildung ist die Überdeckungswahrscheinlichkeit in Abhängigkeit von ${\displaystyle p}$ dargestellt. Das Clopper-Pearson-Intervall wird übrigens deshalb exakt genannt, weil es eine Überdeckungswahrscheinlichkeit sicherstellt, die für alle ${\displaystyle p}$ tatsächlich größer oder gleich dem geforderten Konfidenzniveau ist. Für die anderen oben besprochenen Approximationen ist das nicht der Fall: hier gibt es oft Überdeckungswahrscheinlichkeiten, die kleiner sind als das geforderte Niveau!

Die Überdeckungswahrscheinlichkeit berechnet man in Abhängigkeit von ${\displaystyle p}$ und ${\displaystyle n}$ als Erwartungswert der Indikatorfunktion ${\displaystyle \mathbf {1} _{[p_{u}(k),p_{o}(k)]}(p)}$, wobei der Träger der Indikatorfunktion von der Zahl der Erfolge ${\displaystyle k}$ abhängt, die Binomialverteilt mit ${\displaystyle B(k|p,n)}$ sind:

${\displaystyle P_{p}(k\in \{0,\ldots ,n\}:p\in C(k))=\sum _{k=0}^{n}B(k|p,n)\cdot \mathbf {1} _{[p_{u}(k),p_{o}(k)]}(p)}$.

Die Indikatorfunktion nimmt den Wert 1 an, wenn ${\displaystyle p}$ im Konfidenzintervall liegt, und sonst den Wert 0. Für ${\displaystyle k=0}$ setzt man ${\displaystyle p_{u}=0}$ und für ${\displaystyle k=n}$ setzt man ${\displaystyle p_{o}=1}$.

Diskussion der Vor- und Nachteile der Verfahren

Die beschriebenen Methoden werden in dem grundlegenden Artikel von Brown/Cai/DasGupta^[8] verglichen. Dort wird das Standard-Intervall auch Wald-Intervall genannt (nach Abraham Wald). Brown/Cai/DasGupta empfehlen drei Intervall-Methoden: für größere Fallzahlen das Agresti-Coull-Intervall und für kleinere Fallzahlen das Wilson-Intervall und das Jeffreys-Intervall, welches wir hier nicht besprochen haben.^[9] Für einen graphischen Vergleich der oberen und unteren Grenzen für die vier Methoden siehe auch die Abbildung am Anfang dieser Seite und die folgenden vier Abbildungen, welche eine Überdeckungswahrscheinlichkeit kleiner ${\displaystyle \gamma =95\%}$ rot einfärben, eine Überdeckungswahrscheinlichkeit größer gleich ${\displaystyle \gamma }$ in grün:

• 
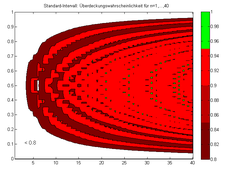  Beim Standard-Intervall liegt die Überdeckungswahrscheinlichkeit für n=1,…,40 fast immer unter dem geforderten Konfidenzniveau.
• 
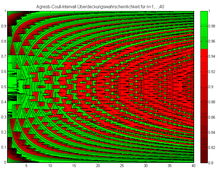  Die Überdeckungswahrscheinlichkeit für das Agresti-Coull-Intervall für n=1,…,40.
• 
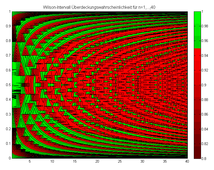  Die Überdeckungswahrscheinlichkeit für das Wilson-Intervall für n=1,…,40.
• 
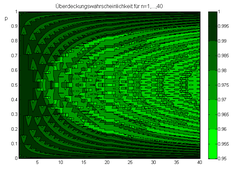  Für n=1,…,40 ist hier die Überdeckungswahrscheinlichkeit für das Clopper-Pearson-Intervall aufgetragen. Sie ist stets größer als γ=0,95.

Literatur

• Alan Agresti, Brent A. Coull: Approximate is better than 'exact' for interval estimation of binomial proportions. In: The American Statistician. 52, 1998, S. 119–126. doi:10.1080/00031305.1998.10480550 JSTOR:2685469
• Lawrence D. Brown, T. Tony Cai, Anirban DasGupta: Interval Estimation for a Binomial Proportion. In: Statistical Science. 16 (2), 2001, S. 101–133. doi:10.1214/ss/1009213286 JSTOR:2676784
• C. Clopper, E. S. Pearson: The use of confidence or fiducial limits illustrated in the case of the binomial. In: Biometrika. 26, 1934, S. 404–413. doi:10.1093/biomet/26.4.404 JSTOR:2331986
• T. D. Ross: Accurate confidence intervals for binomial proportion and Poisson rate estimation. In: Computers in Biology and Medicine. 33, 2003, S. 509–531. doi:10.1016/S0010-4825(03)00019-2
• E. B. Wilson: Probable inference, the law of succession, and statistical inference. In: Journal of the American Statistical Association. 22, 1927, S. 209–212. doi:10.1080/01621459.1927.10502953 JSTOR:2276774
• Norbert Henze: Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls. 8. Auflage. Vieweg+Teubner Verlag, 2010, ISBN 978-3-8348-0815-8, doi:10.1007/978-3-8348-9351-2.
• Ulrich Krengel: Einführung in die Wahrscheinlichkeitstheorie und Statistik. 8. Auflage. Vieweg, 2005.
• Horst Rinne: Taschenbuch der Statistik. Harri Deutsch, 2003.

Weblinks

• Vorsicht bei der sigma-Regel aus: Praxis der Mathematik, Heft 67 (2016) S. 44–47

Einzelnachweise

1. ↑ Die wichtigsten Methoden werden in dem grundlegenden Artikel von Brown/Cai/DasGupta verglichen. Außer den hier angegebenen wird dort noch z. B. das Jeffreys-Intervall besprochen.
2. ↑ Supplement: Loglikelihood and Confidence Intervals. Abgerufen am 14. Juli 2021. 
3. ↑ Siehe hierfür und auch für die Clopper-Pearson- und Wilson-Intervalle Seite 459 des Taschenbuch der Statistik von Horst Rinne.
4. ↑ Siehe Brown/Cai/DasGupta, S. 108
5. ↑ Siehe Krengel, Kapitel 4.7, Abschnitt Konfidenzintervalle für die Erfolgswahrscheinlichkeit
6. ↑ BETAINV-Funktion. microsoft.com, abgerufen am 1. August 2021. 
7. ↑ scipy.stats.beta. docs.scipy.org, abgerufen am 1. August 2021 (englisch). 
8. ↑ Lawrence D. Brown, T. Tony Cai, Anirban DasGupta: Interval Estimation for a Binomial Proportion. In: Statistical Science. Band 16, Nr. 2, 1. Mai 2001, ISSN 0883-4237, doi:10.1214/ss/1009213286. 
9. ↑ Ihr Artikel wird ergänzt durch fünf Kommentare von (1) Alan Agresti und Brent A. Coull (2) George Casella (3) Chris Corcoran und Cyrus Mehta (4) Malay Ghosh (5) Thomas J. Santner und abgeschlossen durch eine Erwiderung von Brown/Cai/DasGupta.