Pollard-Rho-Methode

Die Pollard-Rho-Methoden sind Algorithmen zur Bestimmung der Periodenlänge einer Zahlenfolge, die mit einer mathematischen Funktion berechnet wird. Verschiedene schwierige mathematische Probleme wie der diskrete Logarithmus und die Faktorisierung lassen sich mit diesen Methoden berechnen. Eine optimierte Variante der Pollard-Rho-Methode wurde von John M. Pollard im Jahre 1975 zur Primfaktorzerlegung entwickelt. Derartige Verfahren lassen sich auch zur Berechnung von Kollisionen in Hash-Funktionen anwenden.

Bei den Pollard-Rho-Methoden werden Folgen von Teilergebnissen berechnet. Ab einem bestimmten Punkt wiederholt sich ein Teil dieser Teilergebnisse nur noch. Man kann die Teilergebnisse grafisch so anordnen, dass sich die Gestalt des Buchstaben ρ (Rho) erkennen lässt. Daraus leitet sich die Bezeichnung der Methoden ab.

Gesucht ist ein Primfaktor ${\displaystyle p}$ der Zahl ${\displaystyle n}$. Im Allgemeinen muss dieser Teiler jedoch nicht zwingend eine Primzahl sein. Das Verfahren beruht auf der Erzeugung einer Folge von Pseudozufallszahlen. Zur Erstellung der Zufallsfolge kann eine relativ beliebige Funktion ${\displaystyle f\colon \mathbb {N} \to \mathbb {N} }$ verwendet werden. Es ist lediglich erforderlich, dass aus ${\displaystyle x\equiv y{\pmod {p}}}$ auch ${\displaystyle f(x)\equiv f(y){\pmod {p}}}$ folgt, und dies gilt beispielsweise bereits, wenn ${\displaystyle f}$ durch ein Polynom mit ganzzahligen Koeffizienten gegeben ist.

Die Folge startet mit einem weitgehend beliebig wählbaren Startwert ${\displaystyle x_{0}}$. Die weiteren Werte werden iterativ berechnet gemäß

${\displaystyle x_{i}=f(x_{i-1})}$

Die Funktionswerte modulo ${\displaystyle p}$ können maximal die ${\displaystyle p}$ verschiedenen Werte ${\displaystyle 0,1,2,\ldots ,p-1}$ annehmen. Tritt einer dieser Werte erneut auf, so wiederholen sich anschließend diese Werte modulo ${\displaystyle p}$. Dies geschieht spätestens nach ${\displaystyle p}$ Iterationen und im Mittel nach etwa ${\displaystyle {\sqrt {p}}}$ Iterationen. Aus denselben Gründen kann man nach etwa ${\displaystyle {\sqrt {n}}}$ Iterationen erwarten, dass sich die Werte modulo ${\displaystyle n}$ wiederholen. Wenn bereits bekannt ist, dass ${\displaystyle n}$ einen kleinen Primfaktor hat, ist ${\displaystyle {\sqrt {p}}}$ erheblich kleiner als ${\displaystyle {\sqrt {n}}}$, so dass gehofft werden darf, dass die Wiederholung modulo ${\displaystyle p}$ erheblich früher als die Wiederholung modulo ${\displaystyle n}$ einsetzt.

Bei einer derart berechneten Zahlenfolge mit endlich vielen möglichen Funktionswerten werden zunächst in einer Vorperiode einige Werte

${\displaystyle x_{0},x_{1},\ldots ,x_{k-1}}$

angenommen. Sobald ein Wert wiederholt auftritt, wiederholen sich die Werte anschließend zyklisch

${\displaystyle x_{k},x_{k+1},\ldots ,\left(x_{k+l}=x_{k}\right),x_{k+1},\ldots }$

Dieses Verhalten der Folge gab der Methode ihren Namen, da man sich die Periode wie einen Kreis vorstellen kann und die Folgenglieder am Anfang wie einen Stängel, der in den Kreis hineinführt. Graphisch sieht das aus wie der griechische Buchstabe ρ.

Haben zwei Werte ${\displaystyle x}$ und ${\displaystyle y}$ modulo ${\displaystyle p}$ aus der Folge den gleichen Wert, für die folglich ${\displaystyle x\equiv y{\pmod {p}}\ }$ gilt, so ergibt der größte gemeinsame Teiler ${\displaystyle \operatorname {ggT} (x-y,n)}$ ein Vielfaches von ${\displaystyle p}$ und oftmals einen echten Teiler von ${\displaystyle n}$.

Es ist jedoch sehr aufwändig, alle Zahlenwerte auf diese Weise zu vergleichen. Eine optimierte Variante der Pollard-Rho-Methode berechnet daher zur Bestimmung der Periodenlänge zwei Folgen. Eine Folge

${\displaystyle x=(x_{1},x_{2},x_{3},x_{4},\ldots )}$

und die zweite Folge

${\displaystyle y=(y_{1},y_{2},y_{3},y_{4},\ldots )=(x_{2},x_{4},x_{6},x_{8},\ldots )}$

Durch diesen Trick kann der Vergleich sehr vieler Funktionswerte vermieden werden. Es muss jetzt nicht für alle Paare ${\displaystyle (x_{i},x_{j})}$ der größte gemeinsame Teiler ${\displaystyle \operatorname {ggT} (x_{i}-x_{j},n)}$ berechnet werden. Es genügt jeweils, ${\displaystyle \operatorname {ggT} (x_{i}-y_{i},n)}$ bzw. ${\displaystyle \operatorname {ggT} (x_{i}-x_{2i},n)}$ zu berechnen.

Da ${\displaystyle p}$, als ein gesuchter Teiler von ${\displaystyle n}$, unbekannt ist, kann zunächst der Rest der Division durch ${\displaystyle p}$ nicht berechnet werden. Es wird daher nicht die Gleichheit zweier Werte ${\displaystyle x}$ und ${\displaystyle y}$ abgefragt, sondern der ${\displaystyle \operatorname {ggT} (x-y,n)}$ berechnet. Falls sich die Werte ${\displaystyle x}$ und ${\displaystyle y}$ nur um ein Vielfaches von ${\displaystyle p}$ unterscheiden, ist der Wert des ${\displaystyle \operatorname {ggT} (x-y,n)}$ ein Vielfaches des gesuchten Teilers ${\displaystyle p}$ von ${\displaystyle n}$. Ganzzahlige Vielfache von ${\displaystyle n}$ sind zugleich ganzzahlige Vielfache von ${\displaystyle p}$ und brauchen deshalb bei der Berechnung nicht berücksichtigt werden. Infolgedessen genügt es die Funktionswerte modulo ${\displaystyle n}$ zu berechnen.

Zur Berechnung der Zahlenfolge kann eine Funktion der Form ${\displaystyle f(x)=x^{2}+const}$ benutzt werden. Durch diese Wahl können nur ein Teil, etwa die Hälfte, der Werte ${\displaystyle 0}$ bis ${\displaystyle p-1}$ bei der Restbildung auftreten, wodurch das frühzeitigere Auftreten der gesuchten Wiederholungen etwas begünstigt wird.

Sei ${\displaystyle n}$ die Zahl, von der ein Primfaktor ${\displaystyle p}$ berechnet werden soll. Bezeichne ${\displaystyle (x_{k})_{k\in \mathbb {N} }}$ eine Folge von Pseudozufallszahlen wie zum Beispiel

${\displaystyle {\begin{aligned}x_{0}&=2\\x_{k+1}&=x_{k}^{2}+c{\pmod {n}}\quad {\text{ mit }}\quad c\not \equiv 0{\pmod {n}}{\text{ und }}c\not \equiv -2{\pmod {n}}.\end{aligned}}}$

Existiert ein echter Primfaktor ${\displaystyle p}$, so gilt

Es gibt einen Index ${\displaystyle i<p}$, so dass ${\displaystyle n>k_{i}>1}$ und ${\displaystyle k_{i}\,|\,n}$ mit ${\displaystyle k_{i}=\operatorname {ggT} (|x_{i}-x_{2i}|,n)}$.

Eingabe: ${\displaystyle n}$ ist die zu faktorisierende Zahl und ${\displaystyle f(x)}$ sei die Pseudo-Zufallsfunktion modulo ${\displaystyle n}$
Ausgabe: Ein nicht-trivialer Faktor von ${\displaystyle n}$ oder eine Fehlermeldung

1. x ← 2, y ← x; d ← 1
2. Solange d = 1:
   1. x ← f(x)
   2. y ← f(f(y))
   3. d ← ggT(|x − y|, n)
3. Wenn 1 < d < n, dann d zurückgeben.
4. Falls d = n, dann „Fehler“ ausgeben.

Anmerkung: Dieser Algorithmus liefert für alle ${\displaystyle n}$, die nur durch 1 und sich selbst teilbar sind, eine Fehlermeldung zurück. Allerdings kann auch für die anderen ${\displaystyle n}$ eine Fehlermeldung zurückgeliefert werden. In diesem Fall wählt man eine andere Funktion ${\displaystyle f(x)}$ und versucht es erneut.

Ist das Ergebnis eine Zahl, so ist diese wirklich auch ein Teiler und damit ein korrektes Ergebnis, wobei dieses im Allgemeinen nicht zwingend eine Primzahl sein muss.

Für ${\displaystyle f}$ wählt man ein Polynom mit einem ganzzahligen Koeffizienten. Eine übliche Funktion ${\displaystyle f(x)}$ für diesen Algorithmus hat folgende Form:

${\displaystyle f(x)=x^{2}+c{\hbox{ mod }}n,\,c\neq 0,-2.}$

Die Zahlenfolgen ${\displaystyle x_{i}{\bmod {p}}}$ und ${\displaystyle x_{2i}{\bmod {p}}}$ können als Pseudo-Zufallsfolgen angesehen werden. Falls ein Zahlenwert erneut auftritt, wiederholen sich zwangsläufig die folgenden Werte. Es können bis zu ${\displaystyle p}$ Werte angenommen werden (bei quadratischem ${\displaystyle f}$ wie oben: bis zu ${\displaystyle {\tfrac {p+1}{2}}}$ Werte). Der Erwartungswert für die Länge eines Zyklus beträgt ${\displaystyle {\sqrt {p}}}$. Die Tatsache, dass weit weniger als ${\displaystyle p}$ Berechnungen erforderlich sind, wird zuweilen Geburtstagsparadoxon genannt.

Der ungünstigste Fall tritt ein, wenn ${\displaystyle n}$ ein Produkt von zwei Primzahlen gleicher Länge ist. Der Algorithmus terminiert dann nach O(n^1/4 polylog(n)) Schritten mit einer Wahrscheinlichkeit von ${\displaystyle {\tfrac {1}{2}}}$. Die Methode ist gut geeignet, um Zahlen mit mehreren kleineren Faktoren zu faktorisieren. Der Algorithmus kann in der gleichen Zeit (mit hoher Wahrscheinlichkeit) eine Zahl mit doppelt so vielen Stellen wie die Probedivision faktorisieren. Der Algorithmus arbeitet exponentiell in der Länge der Eingabe und ist damit asymptotisch langsamer als das Quadratische Sieb und das Zahlkörpersieb.

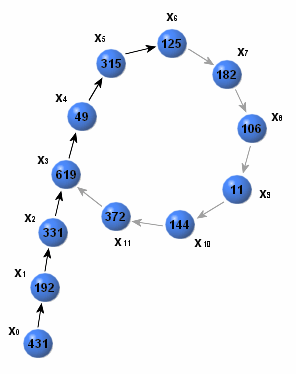
1. Beispiel

Gesucht seien die Faktoren der Zahl ${\displaystyle n=703}$. Wir verwenden die Funktion ${\displaystyle f(x)=x^{2}+23\mod n}$ und den Startwert ${\displaystyle x_{0}=431}$:

Tabelle: Rho-Methode für n = 703

${\displaystyle n=703,\quad f(x)=x^{2}+c}$ mit ${\displaystyle c=23,\quad x_{0}=431}$
${\displaystyle i}$	${\displaystyle x_{i}=f(x_{i-1})}$	${\displaystyle y_{i}=x_{2\cdot i}=f(f(y_{i-1}))}$	${\displaystyle d={\operatorname {ggT} (|x-y|,n})}$
1	192	331	1
2	331	49	1
3	619	125	19
4	49	106	19
5	315	144	19
6	125	619	19
7	182	315	19
8	106	182	19
9	11	11	703
10	144	372	19
11	372	49	19
12	619	125	19

Damit ist die Primfaktorzerlegung von ${\displaystyle 703=19\cdot 37}$ gefunden.

2. Beispiel

Tabelle: Rho-Methode für n = 2717

${\displaystyle n=2717,\quad f(x)=x^{2}+c}$ mit ${\displaystyle c=4,\quad x_{0}=2}$
${\displaystyle i}$	${\displaystyle x_{i}=f(x_{i-1})}$	${\displaystyle y_{i}=x_{2\cdot i}=f(f(y_{i-1}))}$	${\displaystyle d={\operatorname {ggT} (|x-y|,n})}$
1	8	68	1
2	68	277	209
3	1911	2367	19
4	277	68	209
5	657	277	19
6	2367	2367	2717
7	239	68	19
8	68	277	209

Dieses Beispiel zeigt, dass der gefundene Faktor nicht zwingend eine Primzahl sein muss. Der hier gefundene Faktor ist ${\displaystyle 209=11\cdot 19}$.

Mit der beschriebenen Methode konnte 1980 die Fermat-Zahl

${\displaystyle F_{8}=2^{2^{8}}+1=2^{256}+1=1238926361552897\cdot p_{62}}$

faktorisiert werden. ${\displaystyle p_{62}}$ bezeichnet dabei eine (Prim)Zahl mit 62 Stellen, von der erst später bewiesen wurde, dass es sich bei ihr um eine Primzahl handelt.

Die Rho-Methode ist unter dem Namen rho_factorize() Bestandteil der Funktionsbibliothek des Programms ARIBAS von Otto Forster.

• A Monte Carlo Method for Factorization, J.M.Pollard, BIT 15 (1975) 331–334
• An Improved Monte Carlo Factorization Algorithm, R.P.Brent, BIT 20 (1980) 176–184
• Otto Forster: Algorithmische Zahlentheorie. Vieweg, 1996, ISBN 3-528-06580-X

• Pollard Rho Methode in der Mathworld
• Applet für Pollard-Rho Faktorisierung