Järjestelmän dynamiikka

Järjestelmän dynamiikka tai järjestelmädynamiikka kuvaa ajan suhteen riippuvaisen systeemin, kuten esimerkiksi jousi-massa-vaimentimen tai RLC-piirin käyttäytymistä. Dynaamisessa järjestelmässä tulosuureet, kuten jännite tai paine, eivät vaikuta lähtösuureisiin suoraviivaisesti, vaan järjestelmässä saattaa esiintyä värähtelyä ja viivettä sekä systeemin sisäisten osien että tulon ja lähdön välillä. Kun lineaarisessa järjestelmässä tulo- ja lähtösuureet kasvavat ja pienenevät samaan tahtiin, dynaamisessa järjestelmässä lähtösuureen muutosnopeus ja -suunta voivat vaihdella eri nopeudella kuin tulosuure. Järjestelmän dynamiikkaa havainnollistetaan usein mm. Bode-diagrammeilla ja askelvastekuvaajilla.

Dynamiikan kuvaus differentiaaliyhtälöin

Järjestelmän dynamiikkaa kuvataan yleisesti lineaaristen differentiaaliyhtälöryhmien avulla.

Järjestelmän kertaluku määräytyy järjestelmässä olevien energiavarastojen lukumäärän mukaan, mikä näkyy systeemin differentiaalinyhtälön kertaluvusta. Toisin sanoen systeemin kertaluku kertoo systeemin tilamuuttujien lukumäärän. Tilamuuttujana voi olla esimerkiksi virta, jännite, paikka tai nopeus. Yleisimmin systeemin dynamiikkaa kuvaamaan käytetään 1. ja 2. kertaluvun yhtälöitä. Kolmannen ja sitä suurempien kertalukujen yhtälöt ovat matemaattisesti vaikeasti käsiteltäviä, joten ne yleensä esitetään alempien kertalukujen lausekkeiden yhdistelminä. Differentiaaliyhtälöiden yleinen muoto on:

${\displaystyle a_{n}{\frac {d^{n}y}{dt^{n}}}+a_{n-1}{\frac {d^{n-1}y}{dt^{n-1}}}+...+a_{0}y=x(t)}$,

missä x on tulomuuttuja ja y on lähtömuuttuja. Kertoimet a_n,...a₀ ovat vakioita. Järjestelmän dynaamisten ominaisuuksien kuvaus on lineaarinen, joten se voidaan kuvata siirtofunktiomuodossa Laplace-muunnoksen avulla.

Kertaluvut

Järjestelmän dynamiikkaa voidaan analysoida siirtofunktioiden avulla. Siirtofunktio voidaan muodostaan systeemin lähdön ja tulon suhteella ja ne voidaan laijitella kertalukujen perusteella.

0. kertaluku

0. kertaluvun järjestelmässä ei ole yhtään energiavarastoa, joten systeemin lähdön muoto seuraa tulon muotoa. Järjestelmä voi sisältää vahvistusta, jolloin lähdön amplitudi kasvaa tai pienenee.

0. kertaluvun yhtälö on muotoa

${\displaystyle \!a_{0}y=x(t)}$

Siirtofunktio on tällöin muotoa

${\displaystyle {\frac {Y(s)}{X(s)}}=A}$

missä A on vahvistus.

Ideaalinen 0. kertaluvun järjestelmä ei olekaan dynaaminen, vaan staattinen järjestelmä, koska sen käyttäytymiseen vaikuttaa ainoastaan järjestelmän tulo.

Resistiivinen venymäliuska on tietyllä toiminta-alueella esimerkki nollannen kertaluvun järjestelmästä.

1. kertaluku

1. kertaluvun järjestelmä eroaa staattisesta järjestelmästä, koska se kykenee varastoimaan energiaa. Nyt systeemiä ei voida kuvata suoraan tulon perusteella. 1. kertaluvun järjestelmä on yksinkertaisin mahdollinen dynaaminen järjestelmä.

1. kertaluvun yhtälö on muotoa

${\displaystyle a_{1}{\frac {dy}{dt}}+a_{0}y=x(t)}$

Tälle yhtälölle saadaan seuraava siirtofunktio

${\displaystyle {\frac {Y(s)}{X(s)}}={\frac {A}{\tau s+1}}}$,

missä A on järjestelmän vahvistus ja τ aikavakio. Esimerkkejä ensimmäisen kertaluvun järjestelmästä ovat mm. RC-piiri ja nestepohjainen lämpömittari.

2. kertaluku

2. kertaluvun järjestelmässä energia varastoituu tai purkautuu kahden erillisen energiavaraston kautta. Jos energia vaihtelee näiden varastojen välillä, systeemi oskilloi eli värähtelee. Värähtelyn voimakkuus määräytyy systeemin vaimennusvakion suuruudesta. 2. Kertaluvun järjestelmä voidaan tehdä esimerkiksi liittämällä kaksi 1. kertaluvun järjestelmää yhteen.

${\displaystyle a_{2}{\frac {d^{2}y}{d^{2}t}}+a_{1}{\frac {dy}{dt}}+a_{0}y=x(t)}$

Järjestelmän siirtofunktio on yleisessä muodossa

${\displaystyle {\frac {Y(s)}{X(s)}}={\frac {A\omega ^{2}}{s^{2}+2\omega \xi s+\omega ^{2}}}}$,

missä A on järjestelmän vahvistus, ω järjestelmän ominaiskulmataajuus ja ξ vaimennusvakio.

Amplitudin vaimeneminen riippuu vaimennusvakiosta

${\displaystyle \!A=A_{0}e^{-\xi t}}$,

missä A₀ on amplitudin arvo alussa.

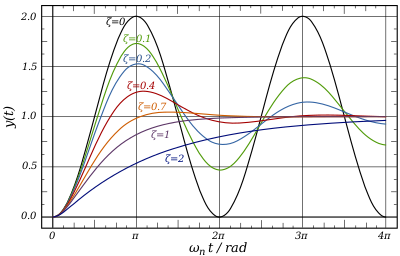
• ξ<0 Järjestelmän amplitudi kasvaa, kunnes se saavuttaa maksimaalisen arvonsa.
• ξ<1 Järjestelmä on alivaimennettu eli värähtelee.
• ξ=1 Järjestelmä on kriittisesti vaimennettu eli se saavuttaa loppuarvonsa nopeimmin eikä värähdä kertaakaan.
• ξ>1 Järjestelmä on ylivaimennettu eli järjestelmä ei värähtele ja saavuttaa huippuarvonsa hitaammin.

Esimerkkejä toisen kertaluvun järjestelmästä ovat mm. RLC-piiri sekä vaimennettu harmoninen värähtelijä.

Järjestelmän tunnuslukuja

Järjestelmän dynaamisia ominaisuuksia kuvataan tunnuslukujen avulla, joista olennaisimpia ovat:

Aikavakio

Aikavakiolla (τ) tarkoitetaan ajanhetkeä, jolloin signaali on saavuttanut 1-e^-1≈63,2% loppuarvostaan. Mitä suurempi järjestelmän aikavakio on, sitä suurempi aika kuluu suhteellisesti tietyn suuruisen muutoksen aikaansaamiseen. Järjestelmä vaimentaa tällöin tulosuureen nopeita muutoksia enemmän ja on dynaamisesti hidas.

Vahvistuskerroin

Vahvistuskerroin (A) ilmaisee systeemin vahvistuksen tai vaimennuksen systeemin saavuttaessa staattisen tilan.

Nousuaika

Aika, jonka kuluessa lähtösuureen arvo kasvaa 10%:n tasolta 90%:n tasolle. Arvoja voidaan tutkia myös muilta väleiltä.

Huippuarvo

Lähtösuureen suurin arvo, joka voi poiketa lopullisesta arvosta riippuen vaimennuksesta.

Huippuaika

Lähtöarvon huippuarvon saavuttamiseen kulunut aika.

Asettumisaika

Aika, jonka kuluttua systeemin lähtö asettuu X%:iin sisään lopullisesta arvostaan ( yleensä käytetään kahden tai viiden prosentin asettumisaikaa ).

Ominaiskulmataajuus

Järjestelmän ominaiskulmataajuus (ω) kertoo systeemin värähtelynopeuden.

Vaimennusvakio

Vaimennusvakio (ξ) kuvaa järjestelmän värähtelyn vaimenemista.

Katso myös

• Bode-diagrammi
• Siirtofunktio
• Impulssi- ja askelvaste
• Laplacen muunnos

Lähteet

• Jokinen Heikki: Mittausjärjestelmien dynamiikka. TUT, 2007. Suomi
• <http://www.mit.tut.fi/mit-1010/Mittausjarjestelmien-dynamiikka.pdf^{[vanhentunut linkki]}>, "Heikki Jokinen"
• <http://autsys.aalto.fi/pub/control.tkk.fi/Kurssit/Verkkokurssit/AS-74.2111/mallit/oppitunti2/jaottelu.html>
• <http://web.mit.edu/sysdyn/sd-intro/>