Houle trochoïdale

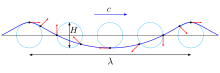
En dynamique des fluides, la houle trochoïdale est une solution exacte des équations d'Euler. Découverte en 1802 par le baron von Gerstner, elle décrit les ondes de gravité de forme périodique qui se propagent à la surface d'un fluide incompressible de profondeur infinie, en régime permanent. La surface libre de l'écoulement est une cycloïde (ou trochoïde, pour reprendre le terme de Gerstner).

C’est un exemple classique d'écoulement tourbillonnaire, et d'utilisation des coordonnées lagrangiennes. Le tourbillon est l’enveloppe des trajectoires des particules de fluide, qui ici sont des cercles dont le rayon varie avec la profondeur. Cette hypothèse n’est pas conforme aux observations expérimentales qui se manifestent par la dérive de Stokes. D’autre part, la vitesse de phase est, dans ce modèle, indépendante de l’amplitude de la houle, anomalie qui a motivé l'étude théorique d'ondes non-linéaires ensuite (telles l’onde de Stokes et l’onde cnoïdale). Pour ces raisons (et nonobstant le fait que ce modèle simple ne peut être adapté à un écoulement en profondeur finie), la houle trochoïdale ne présente plus aujourd’hui qu'un intérêt théorique et didactique^[a].

Elle est cependant encore utilisée en infographie pour le rendu réaliste de vagues. Le champ est étendu à deux dimensions, en utilisant fréquemment un algorithme de transformée de Fourier rapide pour l’animation (temps réel)^[1].

Hypothèses et description

On recherche un écoulement permanent et périodique dans l’espace, et l’on utilise une description lagrangienne. On suppose^[2],[3] :

1. l'écoulement se fait selon des rouleaux cylindriques d'axe horizontal, ce qui élimine une dimension d'espace (déformations planes) ;
2. au repos, les éléments homologues du liquide occupent des droites horizontales à la profondeur ${\displaystyle y}$ ;
3. toutes les particules du liquide orbitent autour de cercles de centre fixe et de rayon ${\displaystyle r(y)}$ avec une pulsation uniforme ;
4. Le rayon ${\displaystyle r(y)}$ est une fonction décroissante ;
5. Le déphasage entre deux particules dont les centres de rotation sont alignés horizontalement, est proportionnel à la distance horizontale entre ces centres.

Description mathématique

Le mouvement des particules fluides de la surface est alors^[4],[5],[6]

${\displaystyle {\begin{aligned}X(a,b,t)&=a+{\frac {\mathrm {e} ^{kb}}{k}}\sin \left(k(a+ct)\right),\\Y(a,b,t)&=b-{\frac {\mathrm {e} ^{kb}}{k}}\cos \left(k(a+ct)\right),\end{aligned}}}$

où ${\displaystyle x=X(a,b,t)}$ et ${\displaystyle y=Y(a,b,t)}$ sont les positions des particules fluides dans le plan ${\displaystyle (x,y)}$ à l’instant ${\displaystyle t}$, où ${\displaystyle x}$ est la coordonnée horizontale et ${\displaystyle y}$ la coordonnée verticale (comptée positivement vers le haut, dans la direction opposée à la gravité). Les coordonnées lagrangiennes ${\displaystyle (a,b)}$ repèrent les particules de fluide, ${\displaystyle (x,y)=(a,b)}$ désignent les centres des orbites circulaires décrites par les particules de fluide avec une célérité constante ${\displaystyle c\,\exp(kb).}$ En outre${\displaystyle k=2\pi /\lambda }$ est le nombre d'onde (et ${\displaystyle \lambda }$ la longueur d'onde), tandis que ${\displaystyle c}$ est la vitesse de phase de l’onde dans la direction ${\displaystyle x}$. La vitesse de phase satisfait une relation de dispersion :

${\displaystyle c^{2}={\frac {g}{k}},}$

qui ne dépend pas du creux ${\displaystyle H}$, et cette vitesse de phase ${\displaystyle c}$ est la même que celle de l'onde d'Airy en eau profonde.

Creux et crête

La surface libre étant naturellement une isobare, il suffit pour la déterminer de poser ${\displaystyle b=b_{s}}$, où ${\displaystyle b_{s}}$ est une constante (non-positive). Les vagues les plus hautes correspondent à ${\displaystyle b_{s}=0}$ : leur crête est une ligne de rebroussement. Tandis que l’onde de Stokes (irrotationnelle) d'ordre le plus élevé présente un angle de crête de 120°, celui de la houle trochoïdale est nul^[7].

Le creux de la houle trochoïdale est ${\displaystyle H=(2/k)\exp(kb_{s})}$. C'est une onde spatialement périodique selon ${\displaystyle x}$, de longueur d'onde ${\displaystyle \lambda ;}$ et aussi périodique dans le temps, de période ${\displaystyle T=\lambda /c={\sqrt {2\pi \lambda /g}}.}$

Le tourbillon ${\displaystyle \varpi }$ de la houle trochoïdale est^[6] :

${\displaystyle \varpi (a,b,t)=-{\frac {2\,k\,c\,\mathrm {e} ^{2kb}}{1-\mathrm {e} ^{2kb}}},}$

Il dépend de la profondeur (lagrangienne) ${\displaystyle b}$ et l'on voit qu’il diminue rapidement.

Application à l'infographie

Il est aisé d'étendre les équations ci-dessus à un modèle 2D en surface (donc 3D) pour l'animation des mers et lacs en infographie^[1] car la solution classique de Gerstner satisfait exactement les équations non-linéaires de l'écoulement d'un fluide parfait sous la surface libre ; cependant, l'extension 2D ne satisfera pas, elle, ces équations exactement (quoiqu'elle le fasse approximativement, pour peu que la description lagrangienne linéarisée utilise un potentiel de vitesse). On peut facilement animer une surface aquatique agitée par le vent très efficacement grâce à la transformation de Fourier rapide (FFT). Le rendu est d'autant plus convaincant que la déformation de la surface libre présente des irrégularités (de par la description lagrangienne de l'écoulement): des crêtes effilées et des creux aplatis.

La description mathématique de la surface libre de la houle trochoïdale se fait ainsi^[1]: les coordonnées horizontales étant notées ${\displaystyle x}$ et ${\displaystyle z}$, et la coordonnée verticale, ${\displaystyle y}$, la surface libre moyenne est ${\displaystyle y=0}$ où ${\displaystyle y}$ est comptée positivement vers le haut, dans la direction opposée à la gravité d'intensité ${\displaystyle g}$. La surface libre est décrite par une équation paramétrique de paramètres ${\displaystyle \alpha }$, ${\displaystyle \beta ,}$ et du temps ${\displaystyle t}$ qui sont fonction des coordonnées des points de la surface moyenne : ${\displaystyle (x,y,z)=(\alpha ,0,\beta )}$ autour desquels les particules de fluide de surface tourbillonnent. L'équation paramétrique de la surface libre est ${\displaystyle x=\xi (\alpha ,\beta ,t),}$ ${\displaystyle y=\zeta (\alpha ,\beta ,t)}$ et ${\displaystyle z=\eta (\alpha ,\beta ,t)}$ avec :

${\displaystyle {\begin{aligned}\xi &=\alpha -\sum _{m=1}^{M}{\frac {k_{x,m}}{k_{m}}}\,{\frac {a_{m}}{\tanh \left(k_{m}\,h\right)}}\,\sin \left(\theta _{m}\right),\\\eta &=\beta -\sum _{m=1}^{M}{\frac {k_{z,m}}{k_{m}}}\,{\frac {a_{m}}{\tanh \left(k_{m}\,h\right)}}\,\sin \left(\theta _{m}\right),\\\zeta &=\sum _{m=1}^{M}a_{m}\,\cos \left(\theta _{m}\right)\quad {\text{et}}\\\theta _{m}&=k_{x,m}\,\alpha +k_{z,m}\,\beta -\omega _{m}\,t-\phi _{m},\end{aligned}}}$

où ${\displaystyle \tanh }$ est la fonction tangente hyperbolique, ${\displaystyle M}$ le nombre de composantes d'onde considéré, ${\displaystyle a_{m}}$ l’amplitude des composantes ${\displaystyle {m=1\dots M}}$ et ${\displaystyle \phi _{m}}$ leurs phases. D'autre part ${\displaystyle {k_{m}=\scriptstyle {\sqrt {(k_{x,m}^{2}+k_{z,m}^{2})}}}}$ est le nombre d'onde et ${\displaystyle \omega _{m}}$ la pulsation. Ces deux dernières, ${\displaystyle k_{m}}$ et ${\displaystyle \omega _{m},}$ ne sont pas indépendants du fait de la relation de dispersion :

${\displaystyle \omega _{m}^{2}=g\,k_{m}\,\tanh \left(k_{m}\,h\right),}$

où ${\displaystyle h}$ est la profondeur moyenne de l'écoulement. En eau profonde (${\displaystyle h\to \infty }$) la tangente hyperbolique tend vers un : ${\displaystyle {\tanh(k_{m}\,h)\to 1}}$. Les composantes ${\displaystyle k_{x,m}}$ et ${\displaystyle k_{z,m}}$ du vecteur d'onde horizontal ${\displaystyle {\boldsymbol {k}}_{m}}$ déterminent la direction de propagation de la composante ${\displaystyle m.}$

Le choix des différents paramètres ${\displaystyle a_{m},k_{x,m},k_{z,m}}$ et ${\displaystyle \phi _{m}}$ pour ${\displaystyle {m=1,\dots ,{M},}}$ et de la profondeur moyenne ${\displaystyle h}$ détermine la forme de la surface libre. Un choix raisonné permettra une actualisation rapide par FFT^[8]. Le plus souvent, on sélectionne les nombres d'onde sur un treillis régulier dans l'espace ${\displaystyle (k_{x},k_{z})}$. De là, les amplitudes ${\displaystyle a_{m}}$ et les phases ${\displaystyle \phi _{m}}$ sont arbitraires mais leur spectre de variance-densité définit un certain état de la mer. Enfin, grâce à l'algorithme de FFT, on peut simuler la surface de la mer comme un continuum périodique dans l'espace et dans le temps, en utilisant un algorithme de facétisation ; la périodicité temporelles est simulée par un léger décalage des fréquences ${\displaystyle \omega _{m}}$ donné par ${\displaystyle \omega _{m}=m\,\Delta \omega }$ pour ${\displaystyle {m=1,\dots ,{M}.}}$

Pour le rendu, on a aussi souvent besoin du vecteur normal ${\displaystyle {\boldsymbol {n}}}$ sur un treillis de points pour l'éclairement des facettes. On l'obtient grâce au produit vectoriel (${\displaystyle \times }$) ce qui donne :

${\displaystyle {\boldsymbol {n}}={\frac {\partial {\boldsymbol {s}}}{\partial \alpha }}\times {\frac {\partial {\boldsymbol {s}}}{\partial \beta }}\quad {\text{avec}}\quad {\boldsymbol {s}}(\alpha ,\beta ,t)={\begin{pmatrix}\xi (\alpha ,\beta ,t)\\\zeta (\alpha ,\beta ,t)\\\eta (\alpha ,\beta ,t)\end{pmatrix}}.}$

Le vecteur normal unité est alors ${\displaystyle {\boldsymbol {e}}_{n}={\boldsymbol {n}}/\|{\boldsymbol {n}}\|,}$ où ${\displaystyle \|{\boldsymbol {n}}\|}$ est la norme euclidienne de ${\displaystyle {\boldsymbol {n}}.}$

Notes et références

Notes

Références

Bibliographie

• (de) Theorie der Wellen, Mémoires de l'Académie royale de Bohême, 1804
  • trad. A. Barré de Saint-Venant, « Théorie des vagues », Annales des Ponts et Chaussées, vol. 1,‎ 1887, p. 31-86
• A.D.D. Craik, « The origins of water wave theory », Annual Review of Fluid Mechanics, vol. 36,‎ 2004, p. 1–28 (DOI 10.1146/annurev.fluid.36.050802.122118, Bibcode 2004AnRFM..36....1C)
• W.J.M. Rankine, « On the exact form of waves near the surface of deep water », Philosophical Transactions of the Royal Society of London, vol. 153,‎ 1863, p. 127–138 (DOI 10.1098/rstl.1863.0006)

• Portail de la physique
• Portail du monde maritime