Gabungan (teori himpunan)

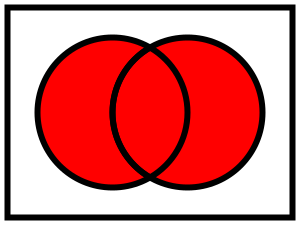
Dalam teori himpunan, gabungan (bahasa Inggris: union) dari koleksi himpunan adalah himpunan semua anggota dalam koleksi.^[1] Gabungan merupakan salah satu operasi dasar, yang dapat menggabungkan atau mengaitkan anggota himpunan ke anggota himpunan lain. Gabungan dilambangkan dengan ∪.

Untuk penjelasan tentang penggunaan simbol lebih lanjut, lihat tabel dari simbol matematika

Gabungan dari dua himpunan

Gabungan dari himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ adalah himpunan anggota yang berada di ${\displaystyle A}$, atau ${\displaystyle B}$, atau bahkan kedua-duanya.^[2] Gabungan dari dua himpunan tersebut dituliskan dalam notasi ungkapan himpunan.^[3]

Sebagai contoh, jika ${\displaystyle A=\{1,3,5,7\}}$ dan ${\displaystyle B=\{1,2,4,6,7\}}$, maka ${\displaystyle A\cup B=\{1,2,3,4,5,6,7\}}$. Contoh yang lebih rumit (meliputi dua himpunan tak terhingga) adalahː

Contoh lainnya, 9 tidak termasuk dalam gabungan dari himpunan bilangan prima ${\displaystyle \{2,3,5,7,11,\dots \}}$ dan juga himpunan dari bilangan genap ${\displaystyle \{2,4,6,8,10.\dots \}}$, sebab 9 bukanlah bilangan prima ataupun bilangan genap.

Himpunan tidak mempunyai anggota identik yang muncul lebih dari satu kali,^[3] karena itu gabungan dari ${\displaystyle \{1,2,3\}}$ dan ${\displaystyle \{2,3,4\}}$ adalah ${\displaystyle \{1,2,3,4\}}$. Banyaknya kemunculan anggota yang identik tersebut tidak mempengaruhi kardinalitas himpunan ataupun isi himpunannya.

Sifat aljabar

Gabungan biner adalah operasi asosiatif. Hal ini berarti bahwa untuk setiap himpunan ${\displaystyle A}$, ${\displaystyle B}$, dan ${\displaystyle C}$, berlaku

Pada rumus di atas, tanda kurung dapat dihilangkan dalam rangka untuk menghindari keambiguan, sehingga dapat ditulis juga sebagai ${\displaystyle A\cup B\cup C}$. Gabungan merupakan operasi komutatif, sehingga himpunan bisa ditulis dalam setiap urutan.^[4] Himpunan kosong adalah anggota identitas untuk operasi gabungan, dalam artian bahwa ${\displaystyle A\cup \varnothing =A}$, untuk setiap himpunan ${\displaystyle A}$. Secara analogi, semua sifat-sifat tersebut diikuti dari logika disjungsi.

Adapun sifat aljabar lainnya, yakni irisan distribusi atas gabungan

dan gabungan distribusi atas irisan^[5]Himpunan kuasa dari himpunan ${\displaystyle U}$, beserta operasi-operasinya, seperti gabungan, irisan, dan komplemen, merupakan aljabar Boole. Dalam aljabar Boole, gabungan dapat dinyatakan dengan rumus yang mengandung operasi irisan dan komplemen.dengan superskrip C melambangkan komplemen dalam himpunan semesta ${\displaystyle U}$.

Gabungan terhingga

Beberapa himpunan dapat diambil secara serentak. Sebagai contoh, gabungan dari tiga himpunan ${\displaystyle A}$, ${\displaystyle B}$, dan ${\displaystyle C}$ mengandung semua anggota dari ${\displaystyle A}$, semua anggota dari ${\displaystyle B}$, dan semua anggota dari ${\displaystyle C}$, dan tidak ada lagi. Dengan demikian, ${\displaystyle x}$ adalah anggota dari ${\displaystyle A\cup B\cup C}$ jika dan hanya jika ${\displaystyle x}$ setidaknya ada di dalam salah satu himpunan ${\displaystyle A}$, ${\displaystyle B}$, dan ${\displaystyle C}$.

Gabungan terhingga adalah gabungan dari jumlah terbatas pada himpunan-himpunan; ungkapan tidak menyiratkan bahwa gabungan himpunan adalah himpunan terbatas.^[6][7]

Gabungan sebarang

Gagasan yang paling umum adalah gabungan dari koleksi himpunan sebarang, yang kadangkala disebut gabungan tak terhingga. Jika ${\displaystyle \mathbf {M} }$ adalah himpunan atau kelas yang anggotanya ada di himpunan, maka ${\displaystyle x}$ adalah gabungan dari ${\displaystyle \mathbf {M} }$ jika dan hanya jika setidaknya ada satu anggota ${\displaystyle A}$ dari ${\displaystyle \mathbf {M} }$ sehingga ${\displaystyle x}$ anggota dari ${\displaystyle A}$.^[8] Ini dapat ditulis dengan menggunakan simbol

Gagasan ini menggolongkan bagian sebelumnya, sebagai contoh, ${\displaystyle A\cup B\cup C}$ adalah gabungan dari koleksi ${\displaystyle \{A,B,C\}}$. Juga, jika ${\displaystyle \mathbf {M} }$ adalah koleksi kosong, maka gabungan dari ${\displaystyle \mathbf {M} }$ adalah himpunan kosong

Notasi

Notasi untuk konsep yang umum sangat bervariasi. Untuk gabungan terhingga dari himpunan ${\displaystyle S_{1},S_{2},S_{3},\dots ,S_{n}}$, acapkali ditulis sebagai ${\displaystyle S_{1}\cup S_{2}\cup S_{3}\cup \dots \cup S_{n}}$ atau

Terdapat bermacam-macam notasi untuk gabungan sembarang, seperti ${\textstyle \bigcup \mathbf {M} }$, ${\textstyle \bigcup _{A\in \mathbf {M} }A}$, atau ${\textstyle \bigcup _{i\in I}A_{i}}$, yang mengacu pada gabungan dari koleksi ${\displaystyle \left\{A_{i}:i\in I\right\}}$, dengan ${\displaystyle I}$ adalah himpunan indeks, dan ${\displaystyle A_{i}}$ adalah himpunan untuk ${\displaystyle i\in I}$. Terdapat sebuah kasus bahwa untuk himpunan indeks ${\displaystyle I}$ yang merupakan himpunan bilangan asli, dapat menggunakan notasiyang mirip seperti jumlah tak terhingga dalam deret.^[8]

Lihat pula

• Aljabar dari himpunan
• Alternasi (teorema bahasa formal), gabungan dari himpunan dari benang.
• Aksioma dari gabungan
• Gabungan penguraian
• Irisan (teori himpunan)
• Operasi biner berulang
• Teori himpunan naif
• Beda setangkup

Catatan

Pranala luar

• Hazewinkel, Michiel, ed. (2001) [1994], "Union of sets", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4 
• Infinite Union and Intersection at ProvenMath Diarsipkan 2023-01-07 di Wayback Machine. De Morgan's laws formally proven from the axioms of set theory.