Curvatura gaussiana

In geometria differenziale, la curvatura gaussiana è una misura della curvatura di una superficie in un punto.

La curvatura gaussiana in un punto ${\displaystyle x}$ di una superficie contenuta nello spazio euclideo è definita come il prodotto delle due curvature principali in ${\displaystyle x}$. La curvatura gaussiana, a differenza delle curvature principali, è una curvatura intrinseca: dipende cioè soltanto dalle distanze fra punti all'interno della superficie, e non da come questa sia contenuta nello spazio tridimensionale. Questo fatto importante è asserito dal teorema egregium di Gauss.

Un altro tipo di curvatura calcolato a partire dalle curvature principali è la curvatura media. A differenza della curvatura di Gauss, la curvatura media non è intrinseca.

Definizione

Hessiano

Una semplice definizione della curvatura gaussiana di una superficie è la seguente. La curvatura gaussiana non cambia se la superficie viene spostata con movimenti rigidi. Per definire la curvatura gaussiana di una superficie ${\displaystyle X}$ in un punto ${\displaystyle P}$, possiamo quindi ruotare ${\displaystyle X}$ in modo che il piano tangente in ${\displaystyle P}$ sia orizzontale. A questo punto la superficie è descritta (almeno localmente, in un intorno di ${\displaystyle P}$) come grafico di una funzione

${\displaystyle f:A\to \mathbb {R} }$

avente come dominio un aperto ${\displaystyle A}$ di ${\displaystyle \mathbb {R} ^{2}}$. La curvatura gaussiana in ${\displaystyle P=(x,y,f(x,y))}$ è il determinante dell'hessiano di ${\displaystyle f}$ in ${\displaystyle (x,y)}$. Perché questa definizione abbia senso, la funzione deve essere differenziabile almeno due volte: l'hessiano è infatti la matrice simmetrica ${\displaystyle 2\times 2}$ data dalle derivate parziali seconde di ${\displaystyle f}$.

Curvature principali

La curvatura gaussiana di una superficie più generale ${\displaystyle X}$ in un punto ${\displaystyle x}$ è il prodotto ${\displaystyle k_{1}k_{2}}$ delle curvature principali. Per definire le curvature principali è necessario fissare una normale alla superficie in ${\displaystyle X}$: poiché la normale opposta dà curvature con segni opposti, il loro prodotto è però ben definito anche senza questa scelta.

Esempi

Curvatura costante

Un piano o un cilindro hanno curvatura gaussiana ovunque nulla. Una sfera di raggio ${\displaystyle r}$ ha curvatura gaussiana ovunque ${\displaystyle 1/r^{2}}$.

Esempio puntuale

La funzione

${\displaystyle f(x,y)=ax^{2}+by^{2}}$

ha gradiente ${\displaystyle (2ax,2by)}$. Il gradiente è nullo nell'origine, e quindi la curvatura gaussiana del grafico ${\displaystyle X}$ di ${\displaystyle f}$ in ${\displaystyle (0,0)}$ è il determinante dell'hessiano. L'hessiano è

${\displaystyle {\begin{pmatrix}2a&0\\0&2b\end{pmatrix}}}$

ed il suo determinante è ${\displaystyle 4ab}$. La curvatura di ${\displaystyle X}$ in ${\displaystyle (0,0)}$ è quindi ${\displaystyle 4ab}$. Questa è ad esempio negativa in presenza di un punto di sella, ove ${\displaystyle a}$ e ${\displaystyle b}$ hanno segni discordi.

Questo metodo per calcolare la curvatura è però funzionante solo in ${\displaystyle (0,0)}$, dove il gradiente si annulla.

Curvatura totale

La curvatura totale di una regione ${\displaystyle A}$ della superficie ${\displaystyle X}$ è l'integrale di superficie

${\displaystyle \int _{A}K\,ds}$

della curvatura gaussiana ${\displaystyle K}$ su ${\displaystyle A}$. La curvatura totale misura quanto si differenzia globalmente la geometria di ${\displaystyle A}$ da quella di una regione piatta sul piano: ad esempio, la curvatura totale di un triangolo geodetico ${\displaystyle T}$ è pari alla differenza fra la somma dei suoi angoli interni (in radianti) e ${\displaystyle \pi }$. In altre parole,

${\displaystyle \sum _{i=1}^{3}\theta _{i}=\pi +\int _{T}K\,ds}$

dove ${\displaystyle \theta _{1},\theta _{2}}$ e ${\displaystyle \theta _{3}}$ sono gli angoli interni.

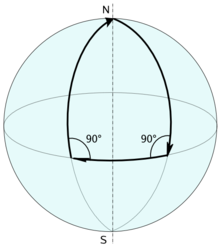
La somma degli angoli di un triangolo su una superficie di curvatura ovunque positiva è maggiore di ${\displaystyle \pi }$, mentre è minore se la superficie ha curvatura ovunque negativa.

Proprietà

Teorema egregium

Per il teorema egregium dimostrato da Gauss nel 1828, la curvatura gaussiana dipende solo dalla sua prima forma fondamentale, cioè dal suo tensore metrico.

La curvatura gaussiana è quindi invariante per isometrie della superficie: si tratta cioè di una proprietà intrinseca della superficie. Una isometria non è necessariamente un movimento rigido dello spazio: un esempio è fornito da un foglio di carta, che può essere arrotolato fino a formare un cilindro. Piano e cilindro sono (almeno localmente) isometrici.

Gauss-Bonnet

Il teorema di Gauss-Bonnet fornisce una stretta connessione fra la curvatura totale di una superficie e la sua topologia. Se ${\displaystyle X}$ è una superficie compatta, il teorema asserisce che

${\displaystyle \int _{X}K\,ds=2\pi \chi (X)}$

cioè la curvatura totale della superficie è pari alla sua caratteristica di Eulero, moltiplicata per ${\displaystyle 2\pi }$.

Ad esempio, una sfera di raggio ${\displaystyle r}$ ha caratteristica 2, e la sua curvatura totale è sempre ${\displaystyle 4\pi }$, indipendentemente da ${\displaystyle r}$. Infatti, è pari al prodotto fra l'area ${\displaystyle 4\pi r^{2}}$ e la curvatura, che è costantemente pari a ${\displaystyle 1/r^{2}}$, poiché entrambe le curvature principali sono ${\displaystyle 1/r}$. Più sorprendentemente, la curvatura totale di una qualsiasi superficie omeomorfa alla sfera (ad esempio, il bordo di un ellissoide) è sempre ${\displaystyle 4\pi }$.

Un toro ha caratteristica di Eulero nulla. Ne segue che la sua curvatura totale è nulla: o questa è ovunque nulla (cosa però impossibile per un toro contenuto nello spazio tridimensionale), oppure presenta zone di curvatura positiva e zone di curvatura negativa.

Bibliografia

• (EN) Manfredo do Carmo, Differential Geometry of Curves and Surfaces, 1976, ISBN 0-13-212589-7.

Voci correlate

• Curvatura principale
• Teorema egregium
• Teorema di Gauss-Bonnet
• Teorema di uniformizzazione di Riemann

Altri progetti

• Wikimedia Commons contiene immagini o altri file su curvatura gaussiana

Collegamenti esterni

• (EN) Gaussian curvature, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Curvatura gaussiana, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica