Distribuzione di Wigner

Distribuzione di Wigner
Funzione di densità di probabilità
Funzione di ripartizione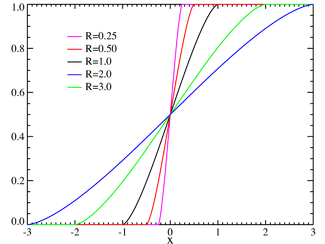
Parametri	${\displaystyle r>0\ }$ (raggio)
Supporto	${\displaystyle [-r,r]\ }$
Funzione di densità	${\displaystyle {\frac {\sqrt {r^{2}-x^{2}}}{{\tfrac {1}{2}}\pi r^{2}}}}$
Funzione di ripartizione	${\displaystyle {\frac {1}{2}}+{\frac {1}{\pi r^{2}}}x{\sqrt {r^{2}-x^{2}}}+{\frac {1}{\pi }}\arcsin {\frac {x}{r}}}$
Valore atteso	${\displaystyle 0\ }$
Mediana	${\displaystyle 0\ }$
Moda	${\displaystyle 0\ }$
Varianza	${\displaystyle {\frac {r^{2}}{4}}}$
Indice di asimmetria	${\displaystyle 0\ }$
Curtosi	${\displaystyle -1\ }$
Entropia	${\displaystyle \log(\pi r)-{\frac {1}{2}}}$
Funzione generatrice dei momenti	${\displaystyle 2{\frac {I_{1}(rt)}{rt}}}$ (funzione di Bessel di primo tipo modificata)
Funzione caratteristica	${\displaystyle 2{\frac {J_{1}(rt)}{rt}}}$ (funzione di Bessel di primo tipo)
Manuale

In teoria delle probabilità la distribuzione di Wigner (detta anche semicircolare, o semiellittica) è una distribuzione di probabilità continua la cui densità di probabilità traccia la metà di un'ellisse.

Prende il nome dal fisico ungherese Eugene Wigner, che la osservò studiando alcune matrici a coefficienti aleatori. ^{[1] [2]}

La distribuzione di Wigner di parametro ${\displaystyle r}$ ha una funzione di densità di probabilità definita sull'intervallo ${\displaystyle [-r,r]}$ e proporzionale alla funzione ${\displaystyle y(x)={\sqrt {r^{2}-x^{2}}}}$, la quale traccia la metà "superiore" della circonferenza ${\displaystyle x^{2}+y^{2}=r^{2}}$. La densità di probabilità è

${\displaystyle f(x)={\frac {\sqrt {r^{2}-x^{2}}}{{\tfrac {1}{2}}\pi r^{2}}}}$,

dove il fattore al denominatore (corrispondente all'area del semicerchio) permette che la probabilità totale sia ${\displaystyle P([-r,r])=1}$. Essendo riscalata rispetto a ${\displaystyle y}$, questa funzione descrive la metà superiore di un'ellisse.

In particolare, se la variabile aleatoria ${\displaystyle X}$ segue la distribuzione di Wigner di parametro 1 allora ${\displaystyle rX}$ segue la distribuzione di Wigner di parametro ${\displaystyle r}$.

La funzione di densità di probabilità della distribuzione di Wigner è simmetrica ed assume valore massimo in 0. Pertanto la speranza matematica, la mediana, la moda e l'indice di asimmetria della distribuzione sono tutti pari a 0, così come tutti i suoi momenti di ordine dispari.

I suoi momenti di ordine pari sono

${\displaystyle \mu _{2k}=E[X^{2k}]={\frac {(2k)!}{k!(k+1)!}}{\frac {r^{2k}}{2^{2k}}}=({\tfrac {r}{2}})^{2k}C_{k}}$,

dove ${\displaystyle C_{k}}$ è il k-esimo numero di Catalan. (In particolare per ${\displaystyle r=2}$ i momenti di ordine pari sono i numeri di Catalan.)

In particolare l'indice di curtosi è

${\displaystyle \gamma _{2}={\frac {\mu _{4}}{\mu _{2}^{2}}}-3=-1}$.

La sua funzione generatrice dei momenti è

${\displaystyle g(t)=E[e^{tX}]=2{\frac {I_{1}(rt)}{rt}}}$,

dove ${\displaystyle I_{1}}$ è una funzione di Bessel di primo tipo modificata.

La sua funzione caratteristica è

${\displaystyle \phi (t)=E[e^{itX}]=2{\frac {J_{1}(rt)}{rt}}}$

dove ${\displaystyle J_{1}}$ è una funzione di Bessel di primo tipo.

La distribuzione di Wigner interviene nella teoria della probabilità libera, per la quale le variabili aleatorie non sono commutative.

In particolare descrive al limite il numero di particolari autovalori di matrici simmetriche ${\displaystyle n\times n}$ i cui coefficienti siano variabili aleatorie indipendente e con una stessa distribuzione di probabilità.

Nella teoria della probabilità "commutativa" una distribuzione di probabilità i cui cumulanti (indicatori "simili" ai momenti) di ordine superiore a due siano nulli è necessariamente una distribuzione normale. Parallelamente, nella teoria ella probabilità libera una distribuzione i cui cumulanti liberi di ordine superiore a due siano tutti nulli è necessariamente una distribuzione di Wigner.

Se la variabile aleatoria ${\displaystyle X}$ segue la distribuzione di Wigner di parametro ${\displaystyle r}$, allora la variabile aleatoria ${\displaystyle {\tfrac {X+r}{2r}}}$ (che assume valori compresi tra 0 e 1) segue la distribuzione Beta di parametri ${\displaystyle ({\tfrac {3}{2}},{\tfrac {3}{2}})}$.

I polinomi di Čebyšëv del secondo tipo, definiti ricorsivamente da ${\displaystyle U_{0}(x)=1}$, ${\displaystyle U_{1}(x)=2x}$ e ${\displaystyle U_{n+1}(x)=2xU_{n}(x)-U_{n-1}(x)}$, sono ortogonali rispetto al prodotto interno

${\displaystyle \langle f,g\rangle =\int _{-1}^{1}f(x)g(x){\sqrt {1-x^{2}}}dx}$.

In teoria dei numeri la distribuzione di Wigner è collegata alla congettura di Sato-Tate: data una curva ellittica senza moltiplicazione complessa ${\displaystyle E}$, si considera il numero ${\displaystyle N_{p}}$ di punti della sua riduzione ${\displaystyle E_{p}}$ in un campo finito con ${\displaystyle p}$ elementi; questo numero è "circa" ${\displaystyle p+1}$, con un errore che non supera ${\displaystyle 2{\sqrt {p}}}$. La congetture di Sato-Tate prevede che al variare dei numeri primi ${\displaystyle p}$ gli errori riscalati ${\displaystyle {\tfrac {N_{p}-(p+1)}{2{\sqrt {p}}}}}$ si distribuiscano secondo la distribuzione di Wigner di parametro 1.

• (EN) Eric W. Weisstein, Wigner's Semicircle Law, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica