余弦定理 (よげんていり、英 : law of cosines, cosine formula )とは、平面 上の三角法 において三角形 の内角の余弦 と辺の長さとの間に成り立つ関係を与える定理である[1] 補題 (第一定理)からなり、第一定理に言及するときそれらは区別される。ただし第一定理と第二定理は実は同値であり、変数の少ない第二定理が計量の上で実用的とされる。そのため、単に余弦定理と言った場合、第二定理を指す。
三角形の角と辺の関係 概要 余弦定理は、内角をその余弦 でとらえる。ここで余弦とは角の余角 に対する正弦のことであり、余角とは、自身の大きさとの和が直角 になる角のことである。
余弦をとらえるのでは直接内角をとらえたことにはならないが、実際には余弦の値に対する内角は一意に決まる。なぜなら、三角形 の内角は 0 < x < π π は円周率 )の範囲を取り、その範囲に制限した余弦関数 y = cos x 狭義減少 の全単射 となるからである。式で表すと逆三角関数 x = arccos y 数値計算 できる。したがって、余弦定理により三角形の内角と辺の関係をとらえることができる。
△ABC において、a = BC, b = CA, c = AB, α = ∠CAB, β = ∠ABC, γ = ∠BCA
a 2 = b 2 + c 2 − 2bc cos α b 2 = c 2 + a 2 − 2ca cos β c 2 = a 2 + b 2 − 2ab cos γ が成り立つ。これらの式が成り立つという命題を余弦定理 、あるいは第二余弦定理 という。
余弦定理は 1つの内角の大きさとそれをはさむ 2辺の長さが分かっていれば、対辺(残りの辺)の長さが決まるという定理である。このことは三角形の合同条件 に対応している。逆に 3辺の長さが分かっていれば
cos α = b 2 + c 2 − a 2 2 b c {\displaystyle \cos \alpha ={\frac {b^{2}+c^{2}-a^{2}}{2bc}}} と余弦について解くことによって内角の大きさを知ることができる。
第二余弦定理において、特に α = π / 2 cos α = 0 ピタゴラスの定理
a 2 = b 2 + c 2 などが導かれる。すなわち、第二余弦定理は、「一般の三角形に対するピタゴラスの定理 」といえる。
歴史 ユークリッド原論 の第2巻命題12では、△ABC を γ が鈍角の鈍角三角形としたとき
c 2 = a 2 + b 2 − 2ab cos γ が成り立つことと、命題13で鋭角三角形の場合が示されている。ユークリッド原論では余弦関数は使われていないが、辺の長さを用いて余弦定理と本質的に同じ命題が示されている。
イスラム世界 では、10世紀に活躍した天文学者 であり数学者 のバッターニー はこれらの結果を球面幾何学 にまで広げ、星の間の距離を測定した。15世紀 には、アル=カーシー が精密な三角関数表を作成し、余弦定理を三角測量 に使いやすい形にした。このためフランス では、余弦定理はアル=カーシーの定理 (Théorème d'Al-Kashi
西洋での余弦定理は16世紀にフランソワ・ビエト によって独自に発見されたことで有名になり、19世紀初頭から現代のような数式で書かれるようになった。
定理 △ABC において、a = BC, b = CA, c = AB, α = ∠CAB, β = ∠ABC, γ = ∠BCA
a = b cos γ + c cos β b = c cos α + a cos γ c = a cos β + b cos α a 2 = b 2 + c 2 − 2bc cos α b 2 = c 2 + a 2 − 2ca cos β c 2 = a 2 + b 2 − 2ab cos γ が成り立つ。
単に余弦定理というと第二余弦定理を指す。
三角形の内角の和は一定(π ラジアン )であるから、2つの内角の大きさが分かっていれば、残りの内角の大きさも定まる。したがって第一余弦定理は、三角形の 2辺と 2つの内角から残りの辺の長さが求められるという定理である。
第一余弦定理の証明 鋭角三角形の場合における第一余弦定理の一つ c = a cos β + b cos α 正弦定理の一部との同値性 第一余弦定理は正弦定理 の一部と同値となる。ここではそれも含めた証明を行う。
辺 b の対角が直角 β = π / 2 cos β = 0 cos β を含む第一余弦定理は
a = b cos γ c = b cos α となる。辺 b は直角三角形 の斜辺であるため、これは余弦関数の定義そのものである。
以下、β と γ は直角ではないとする。すなわち cos β と cos γ は 0 ではないとする。
正弦定理 により
a sin α = b sin β = c sin γ ⋯ ① {\displaystyle {a \over \sin \alpha }={b \over \sin \beta }={c \over \sin \gamma }\quad \cdots \quad {\text{①}}\quad } が、加比の理 から
b cos γ sin β cos γ = c cos β sin γ cos β = b cos γ + c cos β sin β cos γ + sin γ cos β ⋯ ② {\displaystyle {b\cos \gamma \over \sin \beta \cos \gamma }={c\cos \beta \over \sin \gamma \cos \beta }={b\cos \gamma +c\cos \beta \over \sin \beta \cos \gamma +\sin \gamma \cos \beta }\quad \cdots \quad {\text{②}}\quad } が、さらに三角関数の加法定理 から
sin β cos γ + sin γ cos β = sin ( β + γ ) ⋯ ③ {\displaystyle \sin \beta \cos \gamma +\sin \gamma \cos \beta =\sin(\beta +\gamma )\quad \cdots \quad {\text{③}}\quad } が成り立つ。したがって、
a sin α = b sin β = c sin γ ( ∵ ① ) = b cos γ sin β cos γ = c cos β sin γ cos β = b cos γ + c cos β sin β cos γ + sin γ cos β ( ∵ ② ) = b cos γ + c cos β sin ( β + γ ) ( ∵ ③ ) = b cos γ + c cos β sin ( π − α ) ( ∵ α + β + γ = π ) = b cos γ + c cos β sin α {\displaystyle {\begin{aligned}{a \over \sin \alpha }&={b \over \sin \beta }={c \over \sin \gamma }\qquad (\because {\text{①}}\quad )\\&={b\cos \gamma \over \sin \beta \cos \gamma }={c\cos \beta \over \sin \gamma \cos \beta }\\&={b\cos \gamma +c\cos \beta \over \sin \beta \cos \gamma +\sin \gamma \cos \beta }\qquad (\because {\text{②}}\quad )\\&={b\cos \gamma +c\cos \beta \over \sin(\beta +\gamma )}\qquad (\because {\text{③}}\quad )\\&={b\cos \gamma +c\cos \beta \over \sin(\pi -\alpha )}\qquad (\because \alpha +\beta +\gamma =\pi )\\&={b\cos \gamma +c\cos \beta \over \sin \alpha }\end{aligned}}} である。したがって、辺々 sin α {\displaystyle \sin \alpha }
a = b cos γ + c cos β {\displaystyle a=b\cos \gamma +c\cos \beta } が得られる。
逆に、第一余弦定理を仮定して、正弦定理のうち外接円 の半径との関係を除く部分を導出することが、この証明を逆にたどることでできる。
第二余弦定理のみによる導出 第一余弦定理は、第二余弦定理のうち 2式だけから導くことができる。この場合、三平方の定理や正弦定理といった初等幾何の主要な定理は用いずに導いている。
b cos γ + c cos β = b × a 2 + b 2 − c 2 2 a b + c × c 2 + a 2 − b 2 2 c a = a . {\displaystyle b\cos \gamma +c\cos \beta =b\times {\frac {a^{2}+b^{2}-c^{2}}{2ab}}+c\times {\frac {c^{2}+a^{2}-b^{2}}{2ca}}=a.} 第二余弦定理の証明 第一余弦定理との同値性 第二余弦定理は第一余弦定理と同値となる。ここではそれも含めた証明を行う。
△ABC で底辺を BC としたときの高さが
b sin γ = c sin β であることに着目する。
第一余弦定理 a = b cos γ + c cos β の平方 から b sin γ − c sin β (= 0)
a 2 = ( b cos γ + c cos β ) 2 = b 2 cos 2 γ + 2 b c cos γ cos β + c 2 cos 2 β = b 2 ( 1 − sin 2 γ ) + 2 b c cos γ cos β + c 2 ( 1 − sin 2 β ) ( ∵ cos 2 γ + sin 2 γ = cos 2 β + sin 2 β = 1 ) = − ( b 2 sin 2 γ + c 2 sin 2 β ) + b 2 + c 2 + 2 b c cos β cos γ = − ( b sin γ − c sin β ) 2 − 2 b c sin γ sin β + b 2 + c 2 + 2 b c cos β cos γ = − 0 2 + b 2 + c 2 + 2 b c ( cos β cos γ − sin β sin γ ) = b 2 + c 2 − 2 b c cos α . ( ∵ cos β cos γ − sin β sin γ = cos ( β + γ ) = cos ( π − α ) = − cos α ) {\displaystyle {\begin{aligned}a^{2}&=\left(b\cos \gamma +c\cos \beta \right)^{2}\\&=b^{2}\cos ^{2}\gamma +2bc\cos \gamma \cos \beta +c^{2}\cos ^{2}\beta \\&=b^{2}(1-\sin ^{2}\gamma )+2bc\cos \gamma \cos \beta +c^{2}(1-\sin ^{2}\beta )\\&(\because \cos ^{2}\gamma +\sin ^{2}\gamma =\cos ^{2}\beta +\sin ^{2}\beta =1)\\&=-(b^{2}\sin ^{2}\gamma +c^{2}\sin ^{2}\beta )+b^{2}+c^{2}+2bc\cos \beta \cos \gamma \\&=-(b\sin \gamma -c\sin \beta )^{2}-2bc\sin \gamma \sin \beta +b^{2}+c^{2}+2bc\cos \beta \cos \gamma \\&=-0^{2}+b^{2}+c^{2}+2bc(\cos \beta \cos \gamma -\sin \beta \sin \gamma )\\&=b^{2}+c^{2}-2bc\cos \alpha .\\&(\because \cos \beta \cos \gamma -\sin \beta \sin \gamma =\cos(\beta +\gamma )=\cos(\pi -\alpha )=-\cos \alpha )\end{aligned}}} であり第二余弦定理となる。
a > 0
第一余弦定理のみによる導出 第二余弦定理は、第一余弦定理の 3式だけから導くことができる。三平方の定理や正弦定理といった初等幾何の主要な定理は用いず、実質上は三角形の相似だけで導いている。
a 2 = a × a = a × ( b cos γ + c cos β ) = b × a cos γ + c × a cos β = b ( b − c cos α ) + c ( c − b cos α ) ( first cosine theorem ) = b 2 + c 2 − 2 b c cos α . {\displaystyle {\begin{aligned}a^{2}&=a\times a\\&=a\times (b\cos \gamma +c\cos \beta )\\&=b\times a\cos \gamma +c\times a\cos \beta \\&=b(b-c\cos \alpha )+c(c-b\cos \alpha )\\&({\text{first cosine theorem}})\\&=b^{2}+c^{2}-2bc\cos \alpha .\end{aligned}}} なお、特に α = π / 2
三平方の定理による導出 三平方の定理による導出 第二余弦定理は、三平方の定理を利用すれば、三角法 の定理(正弦定理や第一余弦定理など)を使わずに導出することができる。ただし垂線を引くので △ABC の 1つの内角と 90度の大小関係で場合分けする必要がある。
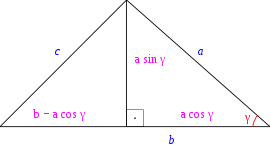
△ABC において、γ ≤ π / 2 B から直線AC に下ろした垂線の足を H とすると、BH = a sin γ , CH = a cos γ , AH = AC − CH = b − a cos γ △ABH に三平方の定理を使えば
c 2 = ( b − a cos γ ) 2 + ( a sin γ ) 2 = b 2 − 2 a b cos γ + a 2 ( cos 2 γ + sin 2 γ ) = a 2 + b 2 − 2 a b cos γ {\displaystyle {\begin{aligned}c^{2}&=\left(b-a\cos \gamma \right)^{2}+\left(a\sin \gamma \right)^{2}\\&=b^{2}-2ab\cos \gamma +a^{2}\left(\cos ^{2}\gamma +\sin ^{2}\gamma \right)\\&=a^{2}+b^{2}-2ab\cos \gamma \end{aligned}}} となる。
γ が鈍角の場合は、「CH = −a cos γ AH = b − a cos γ
ユークリッド原論にみる原型 ユークリッド原論 第1巻命題47においてピタゴラスの定理 が示され、第2巻の最初の方では
(x + y )2 = x 2 + y 2 + 2xy などの二次式の関係が図形問題として述べられる。
ユークリッド原論で扱われているのはこのような数式ではなく x 2 x を一辺の長さとする正方形 の面積として、xy は x と y を辺の長さとする長方形 の面積として表され、正方形や長方形を比べることによって命題が述べられる。 それらを背景として第二余弦定理とほぼ同等な命題が現れる。しかし三角関数 が無かった時代のものなので、現代のように角度と辺の長さの関係として捉えられていたわけではない。余弦が明示的に使われているわけではなく、特定の辺の長さを現代的に余弦を用いて表現すると一致するという意味である。同じ意味で第一余弦定理
c = a cos β + b cos α に対応するものも考えてみると、C から AB に下ろした垂線の足を H としたとき、辺 AB の長さは AH と HB の長さの和ということを示しているだけの定理なので、三角形の辺の長さの関係を表し、特に第一余弦定理を表しているといえる命題といったものはユークリッド原論の中にはない。敢えて言えば、三角形ではなく線分の内分、外分に関する命題ということになる。
第2巻命題12 ユークリッド原論第2巻命題12では AB2 = CA2 + BC2 + 2CA × CH ユークリッド原論第2巻命題12では、鈍角三角形の鈍角に対応する第二余弦定理がピタゴラスの定理 を用いて示されている。現代的に書けば
γ > π / 2 B から AC に下ろした垂線の足を H とする。H は線分 AC 上ではなく AC を C の方へ延長した半直線上にある。d = CH, h = BH△ABH と △CBH にピタゴラスの定理を適用すると
c 2 = ( b + d ) 2 + h 2 d 2 + h 2 = a 2 {\displaystyle {\begin{aligned}c^{2}=\left(b+d\right)^{2}+h^{2}\\d^{2}+h^{2}=a^{2}\end{aligned}}} となり
c 2 = b 2 + 2 b d + d 2 + h 2 = a 2 + b 2 + 2 b d {\displaystyle {\begin{aligned}c^{2}&=b^{2}+2bd+d^{2}+h^{2}\\&=a^{2}+b^{2}+2bd\end{aligned}}} となる。
余弦関数を用いた表現では、鈍角に対する余弦が負になることに注意すれば d = −a cos γ
第2巻命題13 ユークリッド原論第2巻命題13では、鋭角三角形に対する第二余弦定理が示されている。
△ABC において、A から BC に下ろした垂線の足を H とし、p = BH, q = HC, h = AH
第2巻命題7で示されている
a 2 + p 2 = 2 a p + q 2 {\displaystyle a^{2}+p^{2}=2ap+q^{2}} という関係を使うことで
a 2 + ( p 2 + h 2 ) = 2 a p + ( q 2 + h 2 ) {\displaystyle a^{2}+\left(p^{2}+h^{2}\right)=2ap+\left(q^{2}+h^{2}\right)} △ABH と △ACH にピタゴラスの定理を使って
a 2 + c 2 = 2 a p + b 2 {\displaystyle a^{2}+c^{2}=2ap+b^{2}} となる。
余弦関数を用いた表現では p = c cos β
ベクトルの内積による導出 三角形の辺の長さをベクトルの内積 で表し計算すれば、第二余弦定理は自然なものとなる。
a 2 = ‖ BC → ‖ 2 = ‖ AC → − AB → ‖ 2 = ‖ AC → ‖ 2 − 2 AC → ⋅ AB → + ‖ AB → ‖ 2 = AC 2 − 2 AC ⋅ AB cos ∠ BAC + AB 2 = b 2 + c 2 − 2 b c cos α . {\displaystyle {\begin{aligned}a^{2}&=\lVert {\overrightarrow {\text{BC}}}\lVert ^{2}\\&=\lVert {\overrightarrow {\text{AC}}}-{\overrightarrow {\text{AB}}}\lVert ^{2}\\&=\lVert {\overrightarrow {\text{AC}}}\lVert ^{2}-2{\overrightarrow {\text{AC}}}\cdot {\overrightarrow {\text{AB}}}+\lVert {\overrightarrow {\text{AB}}}\lVert ^{2}\\&={\text{AC}}^{2}-2{\text{AC}}\cdot {\text{AB}}\cos \angle {\text{BAC}}+{\text{AB}}^{2}\\&=b^{2}+c^{2}-2bc\cos \alpha .\end{aligned}}} 脚注 [脚注の使い方 ]
^ “余弦定理”. w3e.kanazawa-it.ac.jp . 2022年5月20日 閲覧。 関連項目 外部リンク 世界大百科事典 第2版『余弦定理』 - コトバンク 『第一余弦定理とその3通りの証明』 - 高校数学の美しい物語 『余弦定理とその証明』 - 高校数学の美しい物語 Weisstein, Eric W. "Law of Cosines". mathworld.wolfram.com (英語).