Extreme waarde

In de analyse zijn extreme waarden van een functie de maxima en minima van die functie, dus functiewaarden waar, althans plaatselijk, geen andere functiewaarde boven- dan wel onderuitkomt. We onderscheiden hierin lokale (of relatieve) extrema en globale (of absolute) extrema.

De extremumstelling stelt dat een continue functie ${\displaystyle f}$ op een gesloten interval altijd een minimum en een maximum bereikt.

Formele beschrijving

De functie ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$ bereikt in het punt ${\displaystyle a}$ een

• (lokaal) maximum indien ${\displaystyle f(a)\geq f(x)}$ voor alle ${\displaystyle x}$ in een omgeving van ${\displaystyle a}$.
• (lokaal) minimum indien ${\displaystyle f(a)\leq f(x)}$ voor alle ${\displaystyle x}$ in een omgeving van ${\displaystyle a}$.

Daarin is een omgeving van ${\displaystyle a}$ een verzameling van de vorm:

${\displaystyle \{x\in \mathbb {R} ^{n}\mid |x-a|<\varepsilon \}}$,

voor enige ${\displaystyle \varepsilon >0}$.

We spreken respectievelijk over een globaal maximum of minimum indien het gestelde geldt voor alle ${\displaystyle x}$ uit het domein van ${\displaystyle f}$. Als bovenstaande ongelijkheden strikt zijn voor alle ${\displaystyle x}$ ongelijk aan ${\displaystyle a}$, spreekt men over een uniek maximum cq. minimum.

Voorwaarden en eigenschappen

Differentieerbare functies in één veranderlijke

• Indien de differentieerbare functie ${\displaystyle f}$ in ${\displaystyle a}$ een uiterste waarde of extremum bereikt, is de eerste afgeleide gelijk aan nul; ${\displaystyle f'(a)=0.}$

Dit is geen voldoende voorwaarde maar wel een nodige. Opdat ${\displaystyle f}$ een uiterste waarde bereikt in ${\displaystyle a}$ moet de eerste afgeleide er 0 zijn. Omgekeerd is er echter niet noodzakelijk een uiterste waarde waar de afgeleide 0 wordt (zie voorbeeld 2 voor een tegenvoorbeeld). Punten waarin de afgeleide 0 is heten stationaire punten.

• Om tot een voldoende voorwaarde te komen, kan men kijken naar het teken van de afgeleide. Als de afgeleide in ${\displaystyle a}$ van teken wisselt is de functie in ${\displaystyle a}$ extreem. Of de afgeleide van teken wisselt kan eventueel afgelezen worden aan de[tweede afgeleide ${\displaystyle f''(a)}$ als deze bestaat.

Veronderstel dat ${\displaystyle f}$ twee keer differentieerbaar is en dat ${\displaystyle f'(a)=0.}$ Bkijk dan het teken van de tweede afgeleide:

${\displaystyle f''(a)<0}$, dan bereikt ${\displaystyle f}$ een maximum in ${\displaystyle a}$.

${\displaystyle f''(a)>0}$, dan bereikt ${\displaystyle f}$ een minimum in ${\displaystyle a}$.

${\displaystyle f''(a)=0}$, dan kan er geen conclusie getrokken worden.

• De aard van ${\displaystyle a}$ waarvoor ${\displaystyle f'(a)=0}$ kan eveneens bepaald worden met behulp van een tekenoverzicht van ${\displaystyle f'(a)}$

Onderstel dat ${\displaystyle f}$ differentieerbaar is op een omgeving van ${\displaystyle a}$ en dat ${\displaystyle f'(x)}$ aan beide kanten van ${\displaystyle a}$ een vast teken bezit.

Indien de tekens verschillend zijn bereikt ${\displaystyle f}$ een extremum in ${\displaystyle a:}$

${\displaystyle f(a)}$ is een minimum indien het teken van ${\displaystyle f'(a)}$ links van ${\displaystyle a}$ negatief is en rechts van ${\displaystyle a}$ positief.

${\displaystyle f(a)}$ is een maximum indien het teken van ${\displaystyle f'(a)}$ links van ${\displaystyle a}$ positief is en rechts van ${\displaystyle a}$ negatief.

Indien de tekens aan beide kanten van ${\displaystyle a}$ gelijk zijn bereikt ${\displaystyle f}$ geen extremum, er is dan een buigpunt.

• In een extremum van een functie ${\displaystyle y=f(x)}$ is de raaklijn aan de grafiek steeds horizontaal, dus evenwijdig met de ${\displaystyle x}$-as. Dit volgt rechtstreeks uit het feit dat de afgeleide er 0 moet zijn.

Functies van meerdere variabelen

We kunnen bovenstaande redenering uitbreiden naar functies van meerdere variabelen.
Hiervoor maken we gebruik van begrippen als partiële afgeleide en gradiënt.

• Indien ${\displaystyle f}$ differentieerbaar is in ${\displaystyle a}$ en er een extremum bereikt, dan moet de gradiënt van ${\displaystyle f}$ in ${\displaystyle a}$ gelijk zijn aan 0. Dit is equivalent met het feit dat alle partiële afgeleiden van ${\displaystyle f}$ in ${\displaystyle a}$ ook 0 moeten zijn, dus als voor alle ${\displaystyle i=1,2,\ldots ,n}$

${\displaystyle {\frac {\partial f}{\partial x_{i}}}(a)=0}$

Kort:

${\displaystyle \nabla f(a)=0}$

Ook hier levert dit geen voldoende maar wel een nodige voorwaarde voor extrema. Indien er een extremum bereikt wordt is de gradiënt dus altijd 0, maar het omgekeerde geldt niet. Punten waarin de gradiënt 0 is zijn eveneens stationaire punten.

Opmerking

Voor de eenvoud beperken we ons in de volgende punten tot functies van twee variabelen.

• Om tot een voldoende voorwaarde te komen bekijken we ook hier afgeleiden van de tweede orde. We voeren de volgende notaties in

${\displaystyle \alpha \equiv {\frac {\partial ^{2}f}{\partial x^{2}}}(a,b)}$

,

${\displaystyle \beta \equiv {\frac {\partial ^{2}f}{\partial x\partial y}}(a,b)}$

,

${\displaystyle \gamma \equiv {\frac {\partial ^{2}f}{\partial y^{2}}}(a,b)}$

,

${\displaystyle \delta =\beta ^{2}-\alpha \gamma }$

${\displaystyle \delta >0}$, dan bereikt ${\displaystyle f}$ een zadelpunt (geen extremum) in ${\displaystyle (a,b).}$

${\displaystyle \delta <0}$ en ${\displaystyle \alpha >0}$ (of ${\displaystyle \gamma >0}$), dan bereikt ${\displaystyle f}$ een minimum in ${\displaystyle (a,b).}$

${\displaystyle \delta <0}$ en ${\displaystyle \alpha <0}$ (of ${\displaystyle \gamma <0}$), dan bereikt ${\displaystyle f}$ een maximum in ${\displaystyle (a,b).}$

${\displaystyle \delta =0}$: we kunnen niets besluiten.

• In een extremum van een functie ${\displaystyle z=f(x,y)}$ is het raakvlak aan de grafiek steeds horizontaal, dus evenwijdig met het ${\displaystyle xy}$-vlak. Dit volgt rechtstreeks uit het feit dat de gradiënt er 0 moet zijn.

Voorbeelden

Voorbeeld 1

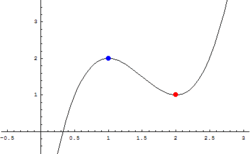
We beschouwen de functie (zie figuur rechts)

${\displaystyle f(x)=2x^{3}-9x^{2}+12x-3}$

We berekenen de eerste afgeleide, stellen deze gelijk aan 0 en lossen op naar x om mogelijke extrema te zoeken

${\displaystyle f'(x)=0\Leftrightarrow 6x^{2}-18x+12=0\Leftrightarrow x=1\ \vee \ x=2}$

Om na te gaan of er in deze punten extrema bereikt worden bepalen we het teken van de tweede afgeleide voor beide punten

${\displaystyle f''(x)=12x-18}$

${\displaystyle f''(1)=-6<0\Rightarrow }$ maximum (blauw)

${\displaystyle f''(2)=+6>0\Rightarrow }$ minimum (rood)

Voorbeeld 2

We beschouwen de functie (zie figuur rechts)

${\displaystyle f(x)=x^{3}}$

We berekenen de eerste afgeleide, stellen deze gelijk aan 0 en lossen op naar ${\displaystyle x}$ om mogelijke extrema te zoeken

${\displaystyle f'(x)=0\Leftrightarrow 3x^{2}=0\Leftrightarrow x=0}$

Om na te gaan of er in dit punt een extremum bereikt wordt bepalen we het teken van de tweede afgeleide in dit punt.

${\displaystyle f''(x)=6x}$

${\displaystyle f''(0)=0\Rightarrow }$ geen extremum (maar een buigpunt) (groen)

Vermits voor elk extremum moet gelden dat de afgeleide 0 is kunnen we besluiten dat deze functie geen extrema heeft.

Voorbeeld 3

We beschouwen de functie (zie figuur rechts)

${\displaystyle f(x,y)=2x^{3}-y^{3}+12x^{2}+27y}$

We berekenen de stationaire punten, dit zijn de punten waarvoor de gradiënt 0 is:

${\displaystyle \left\{{\begin{matrix}{\frac {\partial f}{\partial x}}=0\Leftrightarrow 6x^{2}+24x=0\\{\frac {\partial f}{\partial y}}=0\Leftrightarrow -3y^{2}+27=0\\\end{matrix}}\right.}$

Oplossingen van dit stelsel zijn de punten ${\displaystyle a=(0,3),\ b=(0,-3),\ c=(-4,-3),\ d=(-4,3)}$.

We berekenen δ met voorgenoemde formule voor elk van deze vier punten en vinden

In ${\displaystyle a}$ en in ${\displaystyle c}$ is ${\displaystyle \delta >0}$, dus geen extremum (oranje in de figuur)

In ${\displaystyle b}$ is ${\displaystyle \delta <0}$ en ${\displaystyle \alpha >0}$, dus een minimum (rood in de figuur)

In ${\displaystyle d}$ is ${\displaystyle \delta <0}$ en ${\displaystyle \alpha <0}$, dus een maximum (groen in de figuur)