Metoda gradientu sprzężonego

Porównanie zbieżności metody gradientu prostego (na zielono) i sprzężonego gradientu (na czerwono) dla minimalizacji formy kwadratowej powiązanej z zadanym układem równań liniowych. Metoda sprzężonego gradientu zbiega w co najwyżej n krokach, gdzie n jest rozmiarem macierzy zadanego układu (tutaj n=2).

Metoda gradientu sprzężonego (ang. conjugate gradient method, w skrócie CG) jest algorytmem numerycznym służącym do rozwiązywania niektórych układów równań liniowych. Pozwala rozwiązać te, których macierz jest symetryczna i dodatnio określona. Metoda gradientu sprzężonego jest metodą iteracyjną, więc może być zastosowana do układów o rzadkich macierzach, które mogą być zbyt duże dla algorytmów bezpośrednich takich jak np. rozkład Choleskiego. Takie układy pojawiają się często w trakcie numerycznego rozwiązywania równań różniczkowych cząstkowych.

Metoda gradientu sprzężonego może również zostać użyta do rozwiązania problemu optymalizacji bez ograniczeń.

Opis metody

Rozpatrzmy rozwiązania poniższego układu równań:

Ax = b,

gdzie macierz A n na n jest symetryczna, rzeczywista i dodatnio określona.

Oznaczmy rozwiązanie tego układu przez x*.

Bezpośrednia metoda gradientu sprzężonego

Mówimy, że dwa niezerowe wektory u i v są sprzężone (względem A), jeśli

u T A v = 0 . {\displaystyle \mathbf {u} ^{\mathrm {T} }\mathbf {A} \mathbf {v} =\mathbf {0} .}

Ponieważ A jest symetryczna i dodatnio określona, lewa strona definiuje iloczyn skalarny:

⟨ u , v ⟩ A := ⟨ A T u , v ⟩ = ⟨ A u , v ⟩ = ⟨ u , A v ⟩ = u T A v . {\displaystyle \langle \mathbf {u} ,\mathbf {v} \rangle _{\mathbf {A} }:=\langle \mathbf {A} ^{\mathrm {T} }\mathbf {u} ,\mathbf {v} \rangle =\langle \mathbf {A} \mathbf {u} ,\mathbf {v} \rangle =\langle \mathbf {u} ,\mathbf {A} \mathbf {v} \rangle =\mathbf {u} ^{\mathrm {T} }\mathbf {A} \mathbf {v} .}

Więc, dwa wektory są sprzężone jeśli są ortogonalne względem tego iloczynu skalarnego. Sprzężoność jest relacją symetryczną.

Przypuśćmy, że {pk} jest ciągiem n wzajemnie sprzężonych kierunków. Wtedy pk tworzą bazę Rn, wektor x* będący rozwiązaniem Ax = b możemy przedstawić w postaci:

x ∗ = ∑ i = 1 n α i p i . {\displaystyle \mathbf {x} _{*}=\sum _{i=1}^{n}\alpha _{i}\mathbf {p} _{i}.}

Współczynniki otrzymujemy w następujący sposób:

A x ∗ = ∑ i = 1 n α i A p i = b , {\displaystyle \mathbf {A} \mathbf {x} _{*}=\sum _{i=1}^{n}\alpha _{i}\mathbf {A} \mathbf {p} _{i}=\mathbf {b} ,}
p k T A x ∗ = ∑ i = 1 n α i p k T A p i = p k T b , {\displaystyle \mathbf {p} _{k}^{\mathrm {T} }\mathbf {A} \mathbf {x} _{*}=\sum _{i=1}^{n}\alpha _{i}\mathbf {p} _{k}^{\mathrm {T} }\mathbf {A} \mathbf {p} _{i}=\mathbf {p} _{k}^{\mathrm {T} }\mathbf {b} ,}
α k = p k T b p k T A p k = ⟨ p k , b ⟩ ⟨ p k , p k ⟩ A = ⟨ p k , b ⟩ ‖ p k ‖ A 2 . {\displaystyle \alpha _{k}={\frac {\mathbf {p} _{k}^{\mathrm {T} }\mathbf {b} }{\mathbf {p} _{k}^{\mathrm {T} }\mathbf {A} \mathbf {p} _{k}}}={\frac {\langle \mathbf {p} _{k},\mathbf {b} \rangle }{\quad \langle \mathbf {p} _{k},\mathbf {p} _{k}\rangle _{\mathbf {A} }}}={\frac {\langle \mathbf {p} _{k},\mathbf {b} \rangle }{\quad \|\mathbf {p} _{k}\|_{\mathbf {A} }^{2}}}.}

Co daje nam następującą metodę rozwiązywania równania Ax = b. Najpierw znajdujemy ciąg n sprzężonych kierunków, następnie obliczamy współczynniki α k . {\displaystyle \alpha _{k}.}

Metoda gradientu sprzężonego jako metoda iteracyjna

Jeśli właściwie dobierzemy sprzężone wektory pk, możemy nie potrzebować ich wszystkich do dobrej aproksymacji rozwiązania x*. Możemy więc spojrzeć na CG jak na metodę iteracyjną. Co więcej, pozwoli nam to rozwiązać układy równań, gdzie n jest tak duże, że bezpośrednia metoda zabrałaby zbyt dużo czasu.

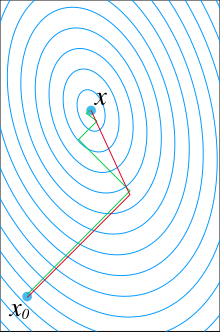
Oznaczmy punkt startowy przez x0. Bez starty ogólności możemy założyć, że x0 = 0 (w przeciwnym przypadku, rozważymy układ Az = b − Ax0). Zauważmy, że rozwiązanie x* minimalizuje formę kwadratową:

f ( x ) = 1 2 x T A x − x T b , x ∈ R n . {\displaystyle f(\mathbf {x} )={\frac {1}{2}}\mathbf {x} ^{\mathrm {T} }\mathbf {A} \mathbf {x} -\mathbf {x} ^{\mathrm {T} }\mathbf {b} ,\quad \mathbf {x} \in \mathbf {R} ^{n}.}

Co sugeruje, by jako pierwszy wektor bazowy p1 wybrać gradient f w x = x0, który wynosi Ax0−b, a ponieważ wybraliśmy x0 = 0, otrzymujemy −b. Pozostałe wektory w bazie będą sprzężone do gradientu (stąd nazwa metoda gradientu sprzężonego).

Niech rk oznacza rezyduum w k-tym kroku:

r k = b − A x k . {\displaystyle \mathbf {r} _{k}=\mathbf {b} -\mathbf {Ax} _{k}.}

Zauważmy, że rk jest przeciwny do gradientu f w x = xk, więc metoda gradientu prostego nakazywałaby ruch w kierunku rk. Tutaj jednak założyliśmy wzajemną sprzężoność kierunków pk, więc wybieramy kierunek najbliższy do rk pod warunkiem sprzężoności. Co wyraża się wzorem:

p k + 1 = r k − p k T A r k p k T A p k p k . {\displaystyle \mathbf {p} _{k+1}=\mathbf {r} _{k}-{\frac {\mathbf {p} _{k}^{\mathrm {T} }\mathbf {A} \mathbf {r} _{k}}{\mathbf {p} _{k}^{\mathrm {T} }\mathbf {A} \mathbf {p} _{k}}}\mathbf {p} _{k}.}

Wynikowy algorytm

Upraszczając, otrzymujemy poniższy algorytm rozwiązujący Ax = b, gdzie macierz A jest rzeczywista, symetryczna i dodatnio określona. x0 jest punktem startowym.

r 0 := b − A x 0 {\displaystyle r_{0}:=b-Ax_{0}}
p 0 := r 0 {\displaystyle p_{0}:=r_{0}}
k := 0 {\displaystyle k:=0}
repeat
α k := r k ⊤ r k p k ⊤ A p k {\displaystyle \alpha _{k}:={\frac {r_{k}^{\top }r_{k}}{p_{k}^{\top }Ap_{k}}}}
x k + 1 := x k + α k p k {\displaystyle x_{k+1}:=x_{k}+\alpha _{k}p_{k}}
r k + 1 := r k − α k A p k {\displaystyle r_{k+1}:=r_{k}-\alpha _{k}Ap_{k}}
if rk+1 jest "wystarczająco mały" then exit loop end if
β k := r k + 1 ⊤ r k + 1 r k ⊤ r k {\displaystyle \beta _{k}:={\frac {r_{k+1}^{\top }r_{k+1}}{r_{k}^{\top }r_{k}}}}
p k + 1 := r k + 1 + β k p k {\displaystyle p_{k+1}:=r_{k+1}+\beta _{k}p_{k}}
k := k + 1 {\displaystyle k:=k+1}
end repeat
Wynikiem jest x k + 1 {\displaystyle x_{k+1}}

Przykład metody gradientu sprzężonego w Octave/MATLAB 

function [x] = conjgrad(A,b,x0)
r = b - A*x0;
w = -r;
z = A*w;
a = (r'*w)/(w'*z);
x = x0 + a*w;

for i = 1:size(A,1);
    r = r - a*z;
    if( norm(r) < 1e-10 )
        break;
    end
    B = (r'*z)/(w'*z);
    w = -r + B*w;
    z = A*w;
    a = (r'*w)/(w'*z);
    x = x + a*w;
end

end

Zobacz też

Bibliografia

  • Metoda gradientu sprzężonego została zaproponowana w:
    • Magnus R.M.R. Hestenes Magnus R.M.R., EduardE. Stiefel EduardE., Methods of Conjugate Gradients for Solving Linear Systems [PDF], „Journal of Research of the National Bureau of Standards”, 6, 49, grudzień 1952 [dostęp 2009-01-20] [zarchiwizowane z adresu 2010-05-05] .
  • Opisy meteody można znaleźć w:
    • Kendell A. Atkinson (1988), An introduction to numerical analysis (2nd ed.), Section 8.9, John Wiley and Sons. ISBN 0-471-50023-2.
    • Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
    • Gene H. Golub and Charles F. Van Loan, Matrix computations (3rd ed.), Chapter 10, Johns Hopkins University Press. ISBN 0-8018-5414-8.

Linki zewnętrzne

  • Conjugate Gradient Method by Nadir Soualem.
  • Preconditioned conjugate gradient method by Nadir Soualem.
  • An Introduction to the Conjugate Gradient Method Without the Agonizing Pain by Jonathan Richard Shewchuk.
  • Iterative methods for sparse linear systems by Yousef Saad
  • LSQR: Sparse Equations and Least Squares by Christopher Paige and Michael Saunders.
Kontrola autorytatywna (projection method for solving system of linear equations):
  • LCCN: sh85031141
  • GND: 4255670-3
  • BnF: 12168447j
  • SUDOC: 030223253
  • J9U: 987007555420405171