Nierówność Jensena przedstawiona graficznie Nierówność Jensena – nierówność między wartością funkcji wypukłej określonej dla kombinacji wypukłej pewnych argumentów a wypukłą kombinacją wartości funkcji w tych argumentach, przy czym obie kombinacje wypukłe mają te same współczynniki. Nazwa nierówności pochodzi od nazwiska Johana Jensena, duńskiego matematyka i inżyniera.
Twierdzenie Dla dowolnych liczb a 1 , a 2 , … , a n ∈ [ 0 , 1 ] , {\displaystyle a_{1},a_{2},\dots ,a_{n}\in [0,1],}
a 1 + a 2 + … + a n = 1 , {\displaystyle a_{1}+a_{2}+\ldots +a_{n}=1,} dla dowolnego przedziału P ⊆ R , {\displaystyle P\subseteq \mathbb {R} ,}
x 1 , x 2 , … , x n ∈ P {\displaystyle x_{1},x_{2},\dots ,x_{n}\in P} i dowolnej funkcji f {\displaystyle f} wypukłej w P , {\displaystyle P,} [1]
f ( ∑ i = 1 n a i x i ) ⩽ ∑ i = 1 n a i f ( x i ) . {\displaystyle f\left(\sum _{i=1}^{n}a_{i}x_{i}\right)\leqslant \sum _{i=1}^{n}a_{i}f(x_{i}).} Dla funkcji wklęsłych prawdziwa jest nierówność w przeciwną stronę.
Dowód Obrazkowy dowód nierówności Jensena. Punkt będący średnią ważoną punktów ( x i , φ ( x i ) ) {\displaystyle (x_{i},\varphi (x_{i}))} otoczce wypukłej , która (z wypukłości ) leży nad wykresem funkcji. Dowód indukcyjny ze względu na n . {\displaystyle n.}
Dla n = 1 {\displaystyle n=1} n = 2 {\displaystyle n=2}
Niech n ⩾ 2. {\displaystyle n\geqslant 2.}
f ( ∑ i = 1 n a i x i ) ⩽ ∑ i = 1 n a i f ( x i ) , {\displaystyle f\left(\sum _{i=1}^{n}a_{i}x_{i}\right)\leqslant \sum _{i=1}^{n}a_{i}f(x_{i}),} gdzie x i {\displaystyle x_{i}} P {\displaystyle P} a 1 + a 2 + … + a n = 1. {\displaystyle a_{1}+a_{2}+\ldots +a_{n}=1.}
Teza indukcyjna to:
f ( ∑ i = 1 n + 1 b i x i ) ⩽ ∑ i = 1 n + 1 b i f ( x i ) , {\displaystyle f\left(\sum _{i=1}^{n+1}b_{i}x_{i}\right)\leqslant \sum _{i=1}^{n+1}b_{i}f(x_{i}),} gdzie x i {\displaystyle x_{i}} P {\displaystyle P} b 1 + b 2 + … + b n + 1 = 1. {\displaystyle b_{1}+b_{2}+\ldots +b_{n+1}=1.}
Niech x i ∈ P {\displaystyle x_{i}\in P} b 1 + b 2 + … + b n + 1 = 1. {\displaystyle b_{1}+b_{2}+\ldots +b_{n+1}=1.} b n + 1 ≠ 0. {\displaystyle b_{n+1}\neq 0.}
f ( ∑ i = 1 n + 1 b i x i ) = f ( b 1 x 1 + ⋯ + b n + 1 x n + 1 ) = {\displaystyle f\left(\sum _{i=1}^{n+1}b_{i}x_{i}\right)=f\left(b_{1}x_{1}+\dots +b_{n+1}x_{n+1}\right)=} = f ( b 1 x 1 + ⋯ + b n − 1 x n − 1 + ( b n + b n + 1 ) ( b n b n + b n + 1 x n + b n + 1 b n + b n + 1 x n + 1 ) ) ⩽ {\displaystyle =f\left(b_{1}x_{1}+\dots +b_{n-1}x_{n-1}+(b_{n}+b_{n+1})({\tfrac {b_{n}}{b_{n}+b_{n+1}}}x_{n}+{\tfrac {b_{n+1}}{b_{n}+b_{n+1}}}x_{n+1})\right)\leqslant } Korzystając z założenia indukcyjnego:
⩽ b 1 f ( x 1 ) + ⋯ + b n − 1 f ( x n − 1 ) + ( b n + b n + 1 ) f ( b n b n + b n + 1 x n + b n + 1 b n + b n + 1 x n + 1 ) ⩽ {\displaystyle \leqslant b_{1}f(x_{1})+\dots +b_{n-1}f(x_{n-1})+(b_{n}+b_{n+1})f({\tfrac {b_{n}}{b_{n}+b_{n+1}}}x_{n}+{\tfrac {b_{n+1}}{b_{n}+b_{n+1}}}x_{n+1})\leqslant } Z definicji funkcji wypukłej:
⩽ b 1 f ( x 1 ) + ⋯ + b n − 1 f ( x n − 1 ) + ( b n + b n + 1 ) b n b n + b n + 1 f ( x n ) + ( b n + b n + 1 ) b n + 1 b n + b n + 1 f ( x n + 1 ) {\displaystyle \leqslant b_{1}f(x_{1})+\dots +b_{n-1}f(x_{n-1})+(b_{n}+b_{n+1}){\tfrac {b_{n}}{b_{n}+b_{n+1}}}f(x_{n})+(b_{n}+b_{n+1}){\tfrac {b_{n+1}}{b_{n}+b_{n+1}}}f(x_{n+1})} = b 1 f ( x 1 ) + ⋯ + b n − 1 f ( x n − 1 ) + b n f ( x n ) + b n + 1 f ( x n + 1 ) = ∑ i = 1 n + 1 b i f ( x i ) , {\displaystyle =b_{1}f(x_{1})+\dots +b_{n-1}f(x_{n-1})+b_{n}f(x_{n})+b_{n+1}f(x_{n+1})=\sum _{i=1}^{n+1}b_{i}f(x_{i}),} co kończy dowód.
Funkcja wklęsła Aby udowodnić nierówność gdy f {\displaystyle f} − f {\displaystyle -f}
( − f ) ( ∑ i = 1 n a i x i ) ⩽ ∑ i = 1 n a i ( − f ) ( x i ) , {\displaystyle (-f)\left(\sum _{i=1}^{n}a_{i}x_{i}\right)\leqslant \sum _{i=1}^{n}a_{i}(-f)(x_{i}),} co jest równoważne nierówności
f ( ∑ i = 1 n a i x i ) ⩾ ∑ i = 1 n a i f ( x i ) . {\displaystyle f\left(\sum _{i=1}^{n}a_{i}x_{i}\right)\geqslant \sum _{i=1}^{n}a_{i}f(x_{i}).} Uwagi W szczególności dla a 1 = a 2 = … = a n = 1 / n {\displaystyle a_{1}=a_{2}=\ldots =a_{n}=1/n} f ( ∑ i = 1 n x i n ) ⩽ ∑ i = 1 n f ( x i ) n . {\displaystyle f\left({\frac {\sum _{i=1}^{n}x_{i}}{n}}\right)\leqslant {\frac {\sum _{i=1}^{n}f(x_{i})}{n}}.} Korzystając z nierówności Jensena, można udowodnić dużą liczbę nierówności, na przykład nierówność między średnią arytmetyczną i geometryczną . Nierówność ma też wiele zastosowań w fizyce i rachunku prawdopodobieństwa . Nierówność Jensena w rachunku prawdopodobieństwa Niech f : R → R {\displaystyle f:\mathbb {R} \to \mathbb {R} } X {\displaystyle X} f , f ( X ) {\displaystyle f,\ f(X)} wartości oczekiwanej nierówność ma postać:
f ( E ( X ) ) ⩽ E ( f ( X ) ) . {\displaystyle f{\big (}\mathbb {E} (X){\big )}\leqslant \mathbb {E} {\big (}f(X){\big )}.} Jeżeli ponadto G {\displaystyle {\mathcal {G}}} warunkowej wartości oczekiwanej nierówność ma postać:
f ( E ( X | G ) ) ⩽ E ( f ( X ) | G ) . {\displaystyle f{\big (}\mathbb {E} (X|{\mathcal {G}}){\big )}\leqslant \mathbb {E} {\big (}f(X){\big |}{\mathcal {G}}{\big )}.} Zobacz też Przypisy ↑ nierówność Jensena , [w:] Encyklopedia PWN [dostęp 2021-10-03] . Bibliografia G.M. Fichtenholz: Rachunek różniczkowy i całkowy . T. 1. Warszawa: Wydawnictwo Naukowe PWN, 2002, s. 263. ISBN 83-01-02175-6 . 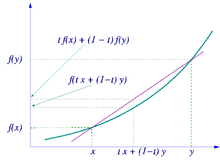

![{\displaystyle a_{1},a_{2},\dots ,a_{n}\in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74bdebccf001085565e9294ee73f6d0e5af2cbf3)











































