Elice Boerdijk–Coxeter
  |
| Răsucite în sens orar, respectiv antiorar |
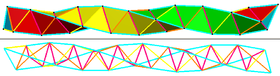 Laturile pot fi colorate în 6 grupuri, 3 elice principale cu pas mare „pe dreapta” (albastru deschis), laturile concave formând o spirală cu pas mic „pe dreapta” (violet) și două elice cu pas mic „pe stânga” (galben și portocaliu) |

Elicea Boerdijk–Coxeter, numită după H. S. M. Coxeter și A. H. Boerdijk, este o împachetare liniară de tetraedre regulate, dispuse astfel încât laturile complexului care aparțin unui singur tetraedru să formeze trei elice împletite. Există două forme chirale, cu înfășurări fie în sensul acelor de ceasornic, fie în sens invers acelor de ceasornic. Spre deosebire de orice altă împachetare de poliedre platonice, elicea Boerdijk–Coxeter nu este repetitivă rotațional în spațiul tridimensional. Chiar și într-un șir infinit de tetraedre, niciun tetraedru nu va avea aceeași orientare, deoarece pasul elicoidal per celulă nu este o fracție rațională a cercului. Totuși, au fost găsite forme modificate ale acestei elice care sunt repetitive rotațional,[1] iar în spațiul cvadridimensional, această spirală se repetă în inele de exact 30 de celule tetraedrice care teselează suprafața 3-sferică a 600-celule, unul dintre cele șase 4-politopuri convexe regulate.
Buckminster Fuller a numit-o „tetrahelix” și a considerat-o cu elemente tetraedrice regulate și neregulate.[2]
Geometrie
Coordonatele vârfurilor elicei Boerdijk–Coxeter compuse din tetraedre cu lungimea muchiei o unitate pot fi scrise sub forma
unde , , și este un întreg arbitrar. Cele două valori diferite ale lui corespund celor două forme chirale. Toate vârfurile sunt situate pe cilindrul cu raza de-a lungul axei z. Având în vedere modul în care se alternează tetraedrele, aceasta dă o răsucire aparentă a la fiecare două tetraedre. Există un alt cilindru, înscris, cu raza în interiorul elicei.[3]
În arhitectură
Forma turnului Art Tower Mito(d) este o elice Boerdijk–Coxeter.
În geometrii din dimensiuni superioare

600-celule se divide în 20 de inele de 30 de tetraedre, fiecare o elice Boerdijk–Coxeter. Când este suprapusă pe curbura 3-sferei, devine periodică, cu o perioadă de zece vârfuri, cuprinzând toate cele 30 de celule. Mulțimea acestor elice din 600-celule reprezintă un fibrat Hopf(d). În timp ce în tridimensional laturile sunt elice, în topologia impusă de 3-sferă sunt geodezice și nu au torsiune. Se spiralează una în jurul celeilalte în mod natural datorită fibratului Hopf. Mulțimea de laturi formează un alt fibrat Hopf discret de 12 inele cu 10 vârfuri fiecare. Acestea corespund inelelor de 10 dodecaedre din dualul 120-celule.
În plus, 16-celule se împarte în două inele de 8 tetraedre, lungi de patru laturi, iar 5-celule are un singur inel degenerat de 5 tetraedre.
| 4-politop | Inele | Tetraedre/inel | Lungime inele | Desfășurată | Proiecție |
|---|---|---|---|---|---|
| 600-celule | 20 | 30 | 30, 103, 152 |  | 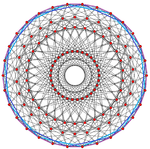 |
| 16-celule | 2 | 8 | 8, 8, 42 |  | |
| 5-celule | 1 | 5 | (5, 5), 5 |  | |
Elice poliedrice înrudite
Piramidele patrulatere echilaterale pot fi și ele înlănțuite împreună într-o spirală, cu două configurații ale vârfurilor, 3.4.3.4 și 3.3.4.3.3.4. Această spirală există ca inel finit de 30 de piramide într-un 600-celule rectificat.
Și piramidele pentagonale echilaterale pot fi înlănțuite, având 3 configurații ale vârfurilor, 3.3.5, 3.5.3.5 și 3.3.3.5.3.3.5:
Note
- ^ Sadler et al. 2013.
- ^ Fuller 1975, 930.00 Tetrahelix.
- ^ en „Tetrahelix Data”.
Bibliografie
- en Coxeter, H. S. M. (). Regular Complex Polytopes
 . Cambridge University Press. ISBN 052120125X.
. Cambridge University Press. ISBN 052120125X. - en Boerdijk, A.H. (). „Some remarks concerning close-packing of equal spheres”. Philips Res. Rep. 7: 303–313.
- en Fuller, R.Buckminster (). Applewhite, E.J., ed. Synergetics. Macmillan.
- en Pugh, Anthony (). „5. Joining polyhedra §5.36 Tetrahelix”. Polyhedra: A visual approach. University of California Press. p. 53. ISBN 978-0-520-03056-5.
- en Sadler, Garrett; Fang, Fang; Kovacs, Julio; Klee, Irwin (). „Periodic modification of the Boerdijk-Coxeter helix (tetrahelix)”. arXiv:1302.1174v1
 [math.MG].
[math.MG]. - en Lord, E.A.; Ranganathan, S. (). „The γ-brass structure and the Boerdijk–Coxeter helix” (PDF). Journal of Non-Crystalline Solids. 334–335: 123–5. Bibcode:2004JNCS..334..121L. doi:10.1016/j.jnoncrysol.2003.11.069. Arhivat din original (PDF) la . Accesat în .
- en Zhu, Yihan; He, Jiating; Shang, Cheng; Miao, Xiaohe; Huang, Jianfeng; Liu, Zhipan; Chen, Hongyu; Han, Yu (). „Chiral Gold Nanowires with Boerdijk–Coxeter–Bernal Structure”. J. Am. Chem. Soc. 136 (36): 12746–52. doi:10.1021/ja506554j
 . PMID 25126894.
. PMID 25126894. - en Lord, Eric A.; Mackay, Alan L.; Ranganathan, S. (). „§4.5 The Boerdijk–Coxeter helix”. New Geometries for New Materials. Cambridge University Press. p. 64. ISBN 978-0-521-86104-5.
- en Sadoc, J.F.; Rivier, N. (). „Boerdijk-Coxeter helix and biological helices”. The European Physical Journal B. 12 (2): 309–318. Bibcode:1999EPJB...12..309S. doi:10.1007/s100510051009.
Vezi și
Legături externe
 | Portal Matematică |
- en Boerdijk-Coxeter helix animation
- en http://www.rwgrayprojects.com/rbfnotes/helix/helix01.html






















