Serie Fourier

Seriile Fourier sunt o unealtă matematică folosită pentru a analiza funcțiile periodice descompunându-le într-o sumă ponderată de funcții sinusoidale componente care sunt uneori denumite armonice Fourier normale, sau pe scurt armonice. Printre generalizări se numără seriile Fourier generalizate.

Seriile Fourier au multe utilizări practice, pentru că manipularea și conceptualizarea coeficienților armonici sunt adesea mai ușoare decât lucrul cu funcția originală. Domeniile de aplicabilitate includ ingineria electrică, analiza undelor, acustică, optică, prelucrarea semnalelor și a imaginilor, și compresia datelor. Folosind uneltele și tehnicile spectroscopiei, de exemplu, astronomii pot deduce compoziția chimică a unei stele prin analizarea componentelor armonice, sau spectrului, stelei care emite lumină. Analog, inginerii pot optimiza proiectarea unui sistem de telecomunicații cu ajutorul informațiilor pe care le oferă componentele spectrale ale unui semnal de date pe care sistemul le transportă.

Seriile Fourier sunt numite după omul de știință și matematicianul francez Joseph Fourier, care le-a folosit în importanta sa lucrare despre conducția termică, Théorie Analytique de la Chaleur (Teoria analitică a căldurii), publicată în 1822.

Definiție

Forma generală

Dată fiind o funcție cu valori complexe f de argument real t, f: R → C, unde f(t) este continuă și derivabilă pe porțiuni, periodică de perioadă T, și integrabilă la pătrat pe intervalul de lungime T dintre ${\displaystyle t_{1}}$ și ${\displaystyle t_{2}}$, adică

${\displaystyle \int _{t_{1}}^{t_{2}}|f(t)|^{2}\,dt<+\infty }$

unde

• ${\displaystyle T=t_{2}-t_{1}}$ este perioada,
• ${\displaystyle t_{1}}$ si ${\displaystyle t_{2}}$ sunt limitele de integrare.

Dezvoltarea în serie Fourier a lui f este

• ${\displaystyle f(t)={\frac {1}{2}}a_{0}+\sum _{n=1}^{\infty }[a_{n}\cos(\omega _{n}t)+b_{n}\sin(\omega _{n}t)]}$

unde, pentru orice întreg nenegativ n,

• ${\displaystyle \omega _{n}=n{\frac {2\pi }{T}}}$     este armonica n (în radiani) a funcției f,
• ${\textstyle a_{0}={\frac {2}{T}}\int _{t_{1}}^{t_{2}}f(t)dt}$
• ${\displaystyle a_{n}={\frac {2}{T}}\int _{t_{1}}^{t_{2}}f(t)\cos(\omega _{n}t)\,dt}$     sunt coeficienții Fourier pari ai lui f, iar
• ${\displaystyle b_{n}={\frac {2}{T}}\int _{t_{1}}^{t_{2}}f(t)\sin(\omega _{n}t)\,dt}$     sunt coeficienții Fourier impari ai lui f.

Echivalent, în formă cu exponențiala complexă,

• ${\displaystyle f(t)=\sum _{n=-\infty }^{+\infty }c_{n}e^{i\omega _{n}t}}$

unde:

• ${\displaystyle c_{n}={\frac {1}{T}}\int _{t_{1}}^{t_{2}}f(t)e^{-i\omega _{n}t}\,dt}$
• ${\displaystyle i}$ este unitatea imaginară, și
• ${\displaystyle e^{i\omega _{n}t}=\cos(\omega _{n}t)+i\sin(\omega _{n}t)}$     conform cu formula lui Euler.

Forma canonică

În cazul special când perioada T = 2π, avem

${\displaystyle \omega _{n}=n\,}$

În acest caz, dezvoltarea în serie Fourier se reduce la o formă deosebit de simplă:

${\displaystyle f(t)={\frac {1}{2}}a_{0}+\sum _{n=1}^{\infty }[a_{n}\cos(nt)+b_{n}\sin(nt)]}$

unde

• ${\displaystyle a_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(t)\cos(nt)\,dt}$
• ${\displaystyle b_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(t)\sin(nt)\,dt}$

oricare ar fi un întreg nenegativ n.

sau, echivalent:

${\displaystyle f(t)=\sum _{n=-\infty }^{+\infty }c_{n}e^{int}}$

unde

• ${\displaystyle c_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t)e^{-int}\,dt={\frac {1}{2}}(a_{n}-ib_{n}).}$

Alegerea formei

Forma pentru perioada T poate fi ușor derivată din cea canonică cu schimbarea de variabilă definită de ${\displaystyle x={\frac {2\pi }{T}}t}$. De aceea, ambele formulări sunt echivalente. Totuși, forma pentru perioada T este preferată în majoritatea cazurilor practice pentru că este direct aplicabilă. Pentru teorie, este preferată forma canonică deoarece este mai elegantă și mai ușor de interpretat matematic.

Exemple

Serii Fourier simple

Fie f periodică de perioadă ${\displaystyle 2\pi }$, cu ${\displaystyle f(x)=x}$ pentru x între −π și π. Se observă că această funcție este o versiune periodică a funcției identitate.

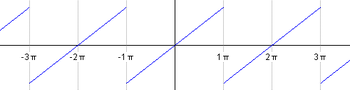
Se vor calcula coeficienții Fourier pentr această funcție.

${\displaystyle {\begin{aligned}a_{n}&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\cos(nx)\,dx\\&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\cos(nx)\,dx\\&{}=0.\end{aligned}}}$

${\displaystyle {\begin{aligned}b_{n}&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\sin(nx)\,dx\\&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\sin(nx)\,dx\\&{}={\frac {2}{\pi }}\int _{0}^{\pi }x\sin(nx)\,dx\\&{}={\frac {2}{\pi }}\left(\left[-{\frac {x\cos(nx)}{n}}\right]_{0}^{\pi }+\left[{\frac {\sin(nx)}{n^{2}}}\right]_{0}^{\pi }\right)\\&{}=2{\frac {(-1)^{n+1}}{n}}.\end{aligned}}}$

Se observă că a_n sunt 0 deoarece ${\displaystyle x\mapsto x\cos(nx)}$ sunt funcții pare. Deci seria Fourier pentru această funcție este:

${\displaystyle f(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]}$

${\displaystyle =2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \forall x\in [-\pi ,\pi ].}$

O aplicație a acestei serii Fourier este calculul funcției Riemann zeta la s = 2; Conform teoremei lui Parseval, avem:

${\displaystyle {\frac {1}{2\pi }}\int _{-\pi }^{\pi }x^{2}dx={\frac {1}{2}}\sum _{n>0}\left[2{\frac {(-1)^{n}}{n}}\right]^{2}}$

de unde rezultă: ${\displaystyle \sum _{n>0}{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}}$.

Ecuația undei

Ecuația undei descrie mișcarea unei coarde vibrante, care poate fi ținuta fixă de capete. Soluția acestei probleme necesită dezvoltarea în serie trigonometrică a unei funcții generale f care dispare la capetele unui interval de la x=0 la x=L. Seria Fourier pentru o asemenea funcție ia forma

${\displaystyle f(x)=\sum _{n=1}^{\infty }b_{n}\sin \left({\frac {n\pi }{L}}x\right)}$

unde

${\displaystyle b_{n}={\frac {2}{L}}\int _{0}^{L}f(x)\sin \left({\frac {n\pi }{L}}x\right)\,dx.}$

Vibrațiile aerului într-o țeavă deschisă la un capăt și închisă la celălalt sunt și ele descrise de ecuația undei. Soluția ei este dată de dezvoltarea în serie Fourier a unei funcții care dispare la x = 0 și care nu mai este derivabilă la x=L. Seria sa Fourier ia forma

${\displaystyle f(x)=\sum _{n=1}^{\infty }b_{n}\sin \left({\frac {(2n+1)\pi }{2L}}x\right)}$

unde

${\displaystyle b_{n}={\frac {2}{L}}\int _{0}^{L}f(x)\sin \left({\frac {(2n+1)\pi }{2L}}x\right)\,dx.}$

Interpretare: descompunerea unei mișcări în rotații

Seriile Fourier au o interpretare cinematică. Funcția ${\displaystyle t\mapsto f(t)}$ poate fi văzută ca mișcare a unui obiect într-un plan (t reprezentând timpul). Deoarece f ia valori complexe, se poate scrie

${\displaystyle f(t)=u(t)+iv(t).\,}$

pentru funcții cu valori reale u și v. În această formă, putem interpreta f ca sumă de translații orizontale și verticale.

De la un moment ${\displaystyle t}$ la un moment ${\displaystyle t+dt}$, unde dt e o perioadă incrementală mică, obiectul se mișcă de la punctul ${\displaystyle A=\left[{\begin{matrix}u(t)\\v(t)\end{matrix}}\right]}$ la punctul ${\displaystyle B=\left[{\begin{matrix}u(t+dt)\\v(t+dt)\end{matrix}}\right]}$, care corespunde unei translații infinitezimale în spațiu după vectorul ${\displaystyle {\overrightarrow {AB}}=\left[{\begin{matrix}u(t+dt)-u(t)\\v(t+dt)-v(t)\end{matrix}}\right]}$. Rezultă că f se poate scrie de forma:

${\displaystyle f(t)=\left[{\begin{matrix}u(dt)-u(0)\\v(dt)-v(0)\end{matrix}}\right]+\left[{\begin{matrix}u(2dt)-u(dt)\\v(2dt)-v(dt)\end{matrix}}\right]+\cdots +\left[{\begin{matrix}u(t+dt)-u(t)\\v(t+dt)-v(t)\end{matrix}}\right]}$

${\displaystyle =\int _{0}^{t}{\frac {1}{dx}}\left[{\begin{matrix}u(x+dx)-u(x)\\v(x+dx)-v(x)\end{matrix}}\right]\,dx.}$

În loc de a vedea pe f ca pe o sumă de translații infinitezimale, o putem vedea ca pe o sumă infinită de rotații cu diferite raze. Această interpretare este convenabilă, mai ales când mișcarea este periodică.

Fie ${\displaystyle \chi _{n}=e^{inx}}$ rotația de n-ture pe secundă, de rază 1). Se dorește scrierea f ca ${\displaystyle f(x)=\sum c_{n}\chi _{n}}$. Se poate demonstra că razele de rotație (coeficienții ${\displaystyle c_{n}}$) sunt exact cei dați în paragraful anterior.

De exemplu, graficul funcției ${\displaystyle f:t\mapsto 2\cos \left({\frac {t}{2}}\right)e^{{\frac {3}{2}}it}}$ este închis, ceea ce înseamnă că funcția este periodică. Bucla de pe curbă sugerează că este suma a două funcții periodice, una cu o perioadă mai scurtă decât cealaltă. Într-adevăr, sepoate scrie: ${\displaystyle f(t)=e^{it}+e^{2it}=\chi _{1}(t)+\chi _{2}(t)}$. Toți coeficienții săi Fourier sunt zero cu excepția ${\displaystyle c_{1}=1}$ și ${\displaystyle c_{2}=1}$. Interpretarea grafică a unei rotații este mult mai dificil de realizat decât a translațiilor, pentru că în loc de a imagina vizual mișcarea dintr-u punct în altul, trebuie adăugată toată mișcarea pentru a avea sens descompunerea (gândirea se face în termeni de frecvență de rotație și nu de timp).

Matematic, adoptarea acestui punct de vedere reprezintă o folosire a seriilor Fourier ca pe o unealtă de înțelegere a operatorilor liniari care comută cu translația. Funcțiile ${\displaystyle \chi _{n}}$ sunt exact caracterele multiplicative ale grupului ${\displaystyle \mathbb {R} /2\pi \mathbb {Z} }$.

Istoric

Context

Seriile Fourier au fost denumite în onoarea lui Joseph Fourier (1768-1830), care a avut importante contribuții la studiul seriilor trigonometrice, după investigații preliminare ale lui Madhava, Nilakantha Somayaji, Jyesthadeva, Leonhard Euler, Jean le Rond d'Alembert și Daniel Bernoulli. El a aplicat această tehnică pentru a găsi soluția pentru ecuația căldurii, publicându-și rezultatele inițiale în 1807 Arhivat în 6 decembrie 2008, la Wayback Machine. și 1811, și publicând lucrarea Théorie analytique de la chaleur în 1822.

Dintr-un punct de vedere modern, rezultatele lui Fourier sunt puțin informale, datorită unei lipse de notație precisă a funcției și integralei la începutul secolului al XIX-lea (de exemplu, la acea vreme nu era lămurit dacă o funcție definită pe două intervale diferite cu două expresii diferite mai era tot o singură funcție). Mai târziu, Dirichlet și Riemann au exprimat rezultatele lui Fourier cu mai mare precizie și rigurozitate.

Un articol revoluționar

În lucrarea lui Fourier intitulată Mémoire sur la propagation de la chaleur dans les corps solides, la paginile 218 și 219, se pot citi următoarele:

${\displaystyle \varphi (y)=a\cos {\frac {\pi y}{2}}+a'\cos 3{\frac {\pi y}{2}}+a''\cos 5{\frac {\pi y}{2}}+\cdots .}$

Înmulțind ambele părți cu ${\displaystyle \cos(2i+1){\frac {\pi y}{2}}}$, și apoi integrând de la ${\displaystyle y=-1}$ la ${\displaystyle y=+1}$ rezultă:

${\displaystyle a_{i}=\int _{-1}^{1}\varphi (y)\cos(2i+1){\frac {\pi y}{2}}\,dy.}$

În aceste câteva rânduri, surprinzător de apropiate de formalismul modern folosit în seriile Fourier, Fourier a revoluționat fără să vrea atât matematica cât și fizica. Deși serii trigonometrice similare mai fuseseră folosite anterior de Euler, d'Alembert, Daniel Bernoulli și Gauss, Fourier a fost primul care a recunoscut că astfel de serii trigonometrice pot reprezenta funcții arbitrare, chiar și funcții cu discontinuități. A trebuit să treacă mulți ani pentru a clarifica această idee, care a condus la importante teorii asupra convergenței, spațiilor de funcții, și analizei armonice.

Lucrarea lui Fourier a fost atât de originală încât, când a trimis-o în 1807, comisia (compusă din alți mari matematicieni ca Lagrange, Laplace, Malus și Legendre, printre alții) a concluzionat: ...maniera în care autorul ajunge la aceste ecuații nu este una scutită de dificultăți și analiza sa încă lasă de dorit la capitolele generalitate și chiar rigoare.

Nașterea analizei armonice

Din vremea lui Fourier până astăzi au fost descoperite multe alte abordări ale definirii și înțelegerii conceptului de serie Fourier, toate fiind corecte și echivalente matematic, dar fiecare punând accent pe alte aspecte ale subiectului. Unele dintre cele mai elegante și mai puternice abordări sunt bazate pe idei și unelte matematice care nu erau disponibile la momentul când Fourier și-a terminat lucrarea. Fourier a definit inițial seriile Fourier pentru funcții reale de argument real, și folosindu-se de funcțiile sinus și cosinus ca bază a descompunerii.

Multe alte transformări de tip Fourier au mai fost definite, extinzând cu alte noi aplicații ideea inițială de reprezentare a oricărei funcții periodice ca suprapunere de armonice. Această arie generală de studiu este uneori numită analiză armonică.

Derivări moderne ale coeficienților Fourier

Metoda lui Fourier de calcul al coeficienților seriei este foarte practică și potrivită problemei pe care o tratează (propagarea căldurii). Totuși, această metodă a fost generalizată între timp la o clasă mult mai largă de probleme: scrierea unei funcții ca sumă de funcții periodice.

Mai exact, dacă f:R → C este o funcție, am vrea să scriem această funcție ca sumă de funcții trigonometrice, i.e. ${\displaystyle f(x)=\sum c_{n}e^{inx}}$. Variantele de alegere a funcțiilor trebuie să fie restrânse pentru ca descompunerea să aibă sens. În primul rând, dacă f este de perioadă T, atunci prin schimbarea variabilelor, se poate studia ${\displaystyle x\mapsto f\left({\frac {T}{2\pi }}x\right)}$ de perioadă 2π. Aceasta simplifică mult notația și permite utilizarea unei forme standard (canonice). Putem restrânge astfel studiul funcțiilor ${\displaystyle x\mapsto f\left({\frac {T}{2\pi }}x\right)}$ la orice interval de lungime 2π, cum ar fi [-π,π].

Luând funcția f:R → C din mulțimea celor continue pe porțiuni, funcții periodice de perioadă 2π cu ${\displaystyle \int _{-\pi }^{\pi }|f(x)|^{2}\,dx<+\infty }$. De fapt, se iau funcții din spațiul Lp L²(μ), unde μ este măsura Lebesgue normalizată a intervalului [-π,π] (astfel încât ${\displaystyle \int _{[-\pi ,\pi ]}f\,d\mu ={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)\,dx}$.

Coeficienți Fourier complecși

Putem transforma L²(μ) într-un spațiu Hilbert, ceea ce este potrivit pentru proiecții ortogonale, prin definirea produsului scalar:

${\displaystyle \langle f,g\rangle =\int _{[-\pi ,\pi ]}f{\overline {g}}\,d\mu ={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x){\overline {g(x)}}\,dx,}$

unde ${\displaystyle {\overline {f(x)}}}$ reprezintă conjugata lui f(x). Vom nota cu ${\displaystyle \|\cdot \|}$ norma asociată.

${\displaystyle E=\{t\mapsto e^{int},n\in \mathbb {Z} \}}$ este o bază ortonormală din L²(μ), deci se poate scrie

${\displaystyle f(x)=\sum _{n\in \mathbb {Z} }\left\langle f,e^{inx}\right\rangle e^{inx}.}$

De regulă se definește ${\displaystyle \forall n\in \mathbb {Z} ,c_{n}=\left\langle f,e^{inx}\right\rangle }$. Aceste numere se numesc coeficienți Fourier complecși. Expresia lor este

${\displaystyle c_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)e^{-inx}\,dx.\,}$

O formulare echivalentă este scrierea f ca sumă de funcții sinus și cosinus.

Coeficienți Fourier reali

Suma din secțiunea anterioară este simetrică în raport cu 0: într-adevăr, cu excepția lui n = 0, un coeficient c_−n corespunde fiecărui coeficientc_n. Astfel ne amintim de formulele

${\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}{\rm {~~~~and~~~~}}\sin x={\frac {e^{ix}-e^{-ix}}{2i}}.}$

Astfel se pot exprima serii Fourier cu funcții cu valori reale. Pentru a face aceasta se observă că

${\displaystyle f(x)=\sum _{n\in \mathbb {Z} }c_{n}e^{inx}=c_{0}+\sum _{n>0}\left[c_{-n}e^{-inx}+c_{n}e^{inx}\right].}$

După înlocuirea lui c_n cu expresia sa și simplificarea rezultatului, obținem

${\displaystyle f(x)=c_{0}+\sum _{n>0}\left[{\frac {1}{\pi }}\left(\int _{-\pi }^{\pi }f(t)\cos \left(nt\right)\,dt\right)\cos \left(nx\right)+{\frac {1}{\pi }}\left(\int _{-\pi }^{\pi }f(t)\sin \left(nt\right)\,dt\right)\sin \left(nx\right)\right].}$

Dacă pentru un număr întreg nenegativ n, definim coeficienții Fourier reali a_n și b_n prin

${\displaystyle a_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\cos \left(nx\right)\,dx,}$

${\displaystyle b_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\sin \left(nx\right)\,dx,}$

obținem:

${\displaystyle f(x)={\frac {a_{0}}{2}}+\sum _{n>0}\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right].}$

Proprietăți

• Următoarele proprietăți se deduc din formula lui Euler: ${\displaystyle e^{ix}=\cos x+i\sin x.\!}$

${\displaystyle a_{n}=c_{n}+c_{-n}}$ și ${\displaystyle b_{n}=i(c_{n}-c_{-n}){\mbox{ for all }}n{\mbox{ and }}\,}$

${\displaystyle c_{n}={\frac {a_{n}-ib_{n}}{2}}}$ și ${\displaystyle c_{-n}={\frac {a_{n}+ib_{n}}{2}}{\mbox{ for all }}n.}$

• Dacă f este o funcție impară, atunci ${\displaystyle a_{n}=0}$ oricare ar fi ${\displaystyle n}$ pentru că ${\displaystyle f(x)\cos \left(n\pi {\frac {x}{T}}\right)}$ este tot pară, deci integrala sa pe intervalul ${\displaystyle [-T,T]}$ este zero. Dacă f este o funcție pară, atunci ${\displaystyle b_{n}=0}$ dintr-un motiv similar.

• Dacă f este continuă pe porțiuni, ${\displaystyle \lim _{n\rightarrow +\infty }c_{n}(f)=0}$, ${\displaystyle \lim _{n\rightarrow +\infty }c_{-n}(f)=0}$, ${\displaystyle \lim _{n\rightarrow +\infty }a_{n}(f)=0}$ și ${\displaystyle \lim _{n\rightarrow +\infty }b_{n}(f)=0.}$

• Dacă f este continuu diferențiabilă de k ori pe porțiuni, atunci se pot calcula ușor coeficienții Fourier ai lui ${\displaystyle f^{(k)}}$ din cei ai lui f:

${\displaystyle c_{n}\left(f^{(k)}\right)=(in)^{k}c_{n}(f),}$

unde ${\displaystyle f^{(k)}}$ este derivata de ordin k a lui f.

• Oricare ar fi un întreg pozitiv al lui k, dacă f este C^k − 1 și C^k pe porțiuni, atunci

${\displaystyle \lim _{n\rightarrow +\infty }|n^{k}c_{n}(f)|=0}$ pentru că ${\displaystyle n^{k}c_{n}(f)=i^{-k}c_{n}\left(f^{(k)}\right)\rightarrow 0.}$

Aceasta înseamnă că seria ${\displaystyle c_{n}(f)}$ este rapid descrescătoare.

Cazul general

Seriile Fourier exploatează periodicitatea funcției f dar dacă f este periodică în mai multe variabile, sau chiar f neperiodică? Aceste probleme i-au condus pe matematicieni și pe fizicienii teoreticieni să încerce să definească seriile Fourier pe orice grup G. Avantajul este, de exemplu, definirea seriilor Fourier pentru funcții de mai multe variabile. Seriile Fourier și transformata Fourier folosite în prelucrarea semnalelor devin astfel cazuri speciale ale acestei teorii și sunt mai ușor de interpretat.

Dacă G grup abelian local compact și T este cercul unitate, se poate defini dualul lui G prin ${\displaystyle {\widehat {G}}=\{\chi :G\rightarrow \mathbb {T} {\mbox{ omomorfism}}\}}$. Acestea constituie mulțimea rotațiilor pe cercul unitate și elementele sale se numesc caractere. Se poate defini un produs scalar ${\displaystyle \langle \cdot ,\cdot \rangle }$ pe C[G] prin: ${\displaystyle \langle \chi _{1},\chi _{2}\rangle =\int _{G}\chi _{1}(g){\overline {\chi _{2}(g)}}\,dg}$. ${\displaystyle {\widehat {G}}}$ este atunci bază ortonormală în C[G] în raport cu acest produs scalar. Fie f :G → C. Coeficienții Fourier ai lui f sunt definiți prin: ${\displaystyle {\widehat {f}}(\chi )=\langle f,\chi \rangle }$ și avem ${\displaystyle f(g)=\int _{\widehat {G}}{\widehat {f}}(\chi )\chi (g)\,d\chi }$. Dacă grupul este discret, atunci integrala se reduce la o sumă.

De exemplu, coeficienții Fourier ai acestui articol sunt obținuți luând G = R/2πZ. Se obține

${\displaystyle {\widehat {G}}=\{\chi _{n}:t\mapsto e^{int},n\in \mathbb {Z} \}}$

și

${\displaystyle c_{n}(f)={\widehat {f}}(\chi _{n})=\int _{G}f(g){\overline {\chi (g)}}\,dg={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t)e^{-int}\,dt.}$

Funcțiile periodice în n dimensiuni pot fi definite pe un tor n-dimensional (funcția ia valoare pe fiecare punct de pe tor). Un astfel de tor este definit prin Tⁿ = Rⁿ/(2πZ)ⁿ. Pentru n = 1 torul este un cerc, pentru n = 2 este produsul cartezian a două cercuri, adică un tor obișnuit. Alegând G = Tⁿ rezultă seria Fourier corespunzătoare.

Aproximarea și convergența seriilor Fourier

Definiția unei serii Fourier

Fie ${\displaystyle \chi _{n}(x)=e^{in\pi {\frac {x}{T}}}}$. Se numește serie Fourier a funcției f seria ${\displaystyle \sum c_{n}\chi _{n}}$. Pentru orice întreg pozitiv N, ${\displaystyle f_{N}(x)=\sum _{n=-N}^{N}c_{n}\chi _{n}(x)}$ se numește a N-a sumă parțială a seriei Fourier a acestei funcții.

Aproximarea cu sume parțiale

Să zicem că dorim să găsim cea mai bună aproximare a lui f folosind doar funcțiile ${\displaystyle \chi _{n}}$ pentru n de la ${\displaystyle -N}$ la N. Fie ${\displaystyle {\mathcal {T}}_{N}=\left\{p=\sum _{n=-N}^{N}x_{n}\chi _{n},x_{n}\in \mathbb {C} \right\}}$. Încercăm sa găsim coeficienții ${\displaystyle (x_{-N},\dots ,x_{N})}$ astfel încât ${\displaystyle \|f-p\|}$ este minim (unde ${\displaystyle \|\cdot \|}$ este norma).

Avem ${\displaystyle \|f-p\|^{2}=\|f\|^{2}-2{\mbox{Re}}\langle f,p\rangle +\|p\|^{2}}$, unde Re(z) notează partea reală a lui z.

${\displaystyle \langle f,p\rangle =\sum _{n=-N}^{N}{\overline {x_{n}}}\langle f,\chi _{n}\rangle .}$

Teorema lui Parseval (ce poate fi dedusă independent din seriile Fourier) dă

${\displaystyle \|p\|^{2}=\sum _{n=-N}^{N}|x_{n}|^{2}.}$

Prin definiție, ${\displaystyle c_{n}=\langle f,\chi _{n}\rangle }$; deci

${\displaystyle \|f-p\|^{2}=\|f\|^{2}+\sum _{n=-N}^{N}\left[|c_{n}-x_{n}|^{2}-|c_{n}|^{2}\right].}$

Este clar că această expresie este minimă pentru ${\displaystyle x_{n}=c_{n}}$ și doar pentru această valoare.

Deci există un singur ${\displaystyle f_{N}\in {\mathcal {T}}_{N}}$ astfel încât

${\displaystyle \|f-f_{N}\|=\min _{p\in {\mathcal {T}}_{N}}\left\{\|f-p\|,p\in {\mathcal {T}}_{N}\right\},}$

este dat de

${\displaystyle f_{N}(x)=\sum _{n=-N}^{N}c_{n}\chi _{n}(x),}$

unde

${\displaystyle c_{n}={\frac {1}{2T}}\int _{-T}^{T}f(t)\chi _{-n}(t)\,dt.}$

Deci cea mai bună aproximare a lui f ce poate fi făcută folosind doar funcțiile ${\displaystyle \chi _{n}(x)=e^{in\pi {\frac {x}{T}}}}$ pentru n de la ${\displaystyle -N}$ la N este exact a N-a sumă parțială a seriei Fourier.

Convergența

În timp ce coeficienții Fourier a_n și b_n pot fi definiți formal pentru orice funcție integrabilă, dacă această funcție converge sau nu la f(x) depinde de proprietățile lui f.

Cel mai simplu răspuns este că pentru ca seria să conveargă, f trebuie să fie integrabilă la pătrat, deci

${\displaystyle \lim _{N\rightarrow \infty }\int _{-\pi }^{\pi }\left|f(x)-\sum _{n=-N}^{N}c_{n}\,\chi _{n}(x)\right|^{2}\,dx=0.}$

Aceasta este convergență în norma dată de spațiul L². Demonstrația acestui rezultat este simplă, spre deosebire de rezultatul mult mai puternic dat de Lennart Carleson conform căruia seriile converg aproape în orice caz.

Există mai multe teste care asigură că seria converge într-un punct dat, de exemplu, dacă funcția este diferențiabilă în x. Nici chiar o mică discontinuitate a derivatei nu constituie o problemă: dacă funcția are derivată la stânga și la dreapta în x, atunci seria Fourier va converge la media limitelor la stânga și la dreapta (dar vezi Fenomenul Gibbs). Totuși, fapt considerat de mulți surprinzător, seria Fourier a unei funcții continue nu trebuie neapărat să fie convergentă în fiecare punct.

Această situație neplăcută este echilibrată de o teoremă a lui Dirichlet care afirmă că dacă f este periodică de perioadă ${\displaystyle 2T}$ și derivată cu derivata continuă, atunci seria ei Fourier converge în fiecare punct și ${\displaystyle \sum _{n\in \mathbb {Z} }c_{n}\chi _{n}(x)={\frac {f(x^{+})+f(x^{-})}{2}}}$, unde ${\displaystyle f(x^{+})=\lim _{t\rightarrow x,t>x}f(x)}$ și ${\displaystyle f(x^{-})=\lim _{t\rightarrow x,t<x}f(x)}$. Dacă f este continuă și cu derivata continuă pe porțiuni, atunci seria Fourier converge uniform.

În 1922, Andrei Kolmogorov a publicat un articol intitulat Une série de Fourier-Lebesgue divergente presque partout Arhivat în 24 martie 2006, la Wayback Machine. în care a dat un exemplu de funcție integrabilă Lebesgue a cărei serie Fourier divere aproape în fiecare punct. Această funcție nu este din ${\displaystyle L^{2}(\mu )}$.

Teoremele lui Plancherel și Parseval

O altă proprietate importantă a seriilor Fourier este Teorema lui Plancherel. Fie ${\displaystyle f,g\in L^{2}(\mu )}$ și ${\displaystyle c_{n}(f),c_{n}(g)}$ coeficienții Fourier complecși corespunzători. Atunci

${\displaystyle \sum _{n\in \mathbb {Z} }c_{n}(f){\overline {c_{n}(g)}}={\frac {1}{2T}}\int _{-T}^{T}f(x){\overline {g(x)}}\,dx}$

unde cu ${\displaystyle {\overline {z}}}$ s-a notat conjugatul lui z.

Teorema lui Parseval, un caz special al teoremei lui Plancherel, afirmă că:

${\displaystyle \sum _{n\in \mathbb {Z} }|c_{n}(f)|^{2}={\frac {1}{2T}}\int _{-T}^{T}|f(x)|^{2}\,dx}$

reformulabilă astfel pentru coeficienți Fourier reali:

${\displaystyle {\frac {a_{0}^{2}}{4}}+{\frac {1}{2}}\sum _{n=1}^{\infty }\left(a_{n}^{2}+b_{n}^{2}\right)={\frac {1}{2T}}\int _{-T}^{T}|f(x)|^{2}\,dx.}$

Aceste teoreme se pot demonstra folosind relațiile de ortogonalitate. Ele pot fi interpretate fizic spunând că scrierea unui semnal ca serie Fourier series nu îi modifică energia.

Bibliografie

• Joseph Fourier, tradusă în engleză de Alexander Freeman (publicată în 1822, tradusă 1878, republicată 2003). The Analytical Theory of Heat. Dover Publications. ISBN 0-486-49531-0.  Verificați datele pentru: |date= (ajutor) republicarea completă din 2003 a traducerii în engleză din 1878 de Alexander Freeman a lucrării lui Fourier Théorie Analytique de la Chaleur, inițial publicată în 1822.
• Yitzhak Katznelson, An introduction to harmonic analysis, Second corrected edition. Dover Publications, Inc., New York, 1976. ISBN 0-486-63331-4
• Felix Klein, Development of mathematics in the 19th century. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert, Springer, Berlin, 1928.
• Walter Rudin, Principles of mathematical analysis, Third edition. McGraw-Hill, Inc., New York, 1976. ISBN 0-07-054235-X
• William E. Boyce and Richard C. DiPrima, Elementary Differential Equations and Boundary Value Problems, Eighth edition. John Wiley & Sons, Inc., New Jersey, 2005. ISBN 0-471-43338-1