Rovina

Rovina je v matematice dvourozměrný geometrický útvar, který si lze představit jako neomezenou dokonale rovnou plochu. Algebraicky vyjádřeno, jde o množinu bodů izomorfní s dvoudimenzionálním lineárním prostorem. Jinak řečeno jde o dvoudimenzionální afinní prostor.

Rovina může být určena třemi různými body, nebo přímkou a bodem, který leží mimo tuto přímku.

Značení

Rovina je buď plocha, na kterou se kreslí (nákresna), nebo se znázorňuje některým rovinným útvarem pomocí některého geometrických promítání. Rovina se označuje malým řeckým písmenem.

Znázornění:

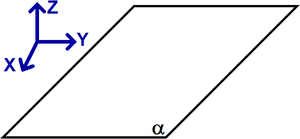
Rovnice roviny

Rovina je množina bodů prostoru, které vyhovují tzv. rovnici roviny, která může být zadána v různých tvarech.

Obecná rovnice roviny

Obecná rovnice roviny má tvar

${\displaystyle ax+by+cz+d=0\,\!}$,

kde koeficienty ${\displaystyle a,\,b,\,c\,\!}$ nejsou současně nulové a jsou to koeficienty normálového vektoru roviny (vektoru kolmého k rovině). Proměnné ${\displaystyle x,\,y,\,z\,\!}$ jsou souřadnice bodu ležícího v rovině.

V případě, že známe tři body ${\displaystyle K,\,L,\,M}$ určující rovinu, obecnou rovnici roviny získáme takto: spočteme vektory ${\displaystyle {\overrightarrow {KL}}}$ a ${\displaystyle {\overrightarrow {KM}}}$, vypočítáme jejich Vektorový součin ze kterého získáme koeficienty ${\displaystyle a,\,b,\,c\,\!}$ a napíšeme obecnou rovnici. Zbývající koeficient d získáme tak, že dosadíme souřadnice bodu K (nebo kteréhokoli jiného bodu ze zadání) do napsané rovnice.

Parametrické vyjádření roviny

Parametrické vyjádření roviny má například vektorový tvar ${\displaystyle X=A+tu+sv\,\!}$, který se dá rozepsat dle složek takto:

${\displaystyle x=A_{1}+tu_{1}+sv_{1}\,\!}$

${\displaystyle y=A_{2}+tu_{2}+sv_{2}\,\!}$

${\displaystyle z=A_{3}+tu_{3}+sv_{3}\,\!}$,

kde ${\displaystyle s,\,t\in R\,\!}$ a ${\displaystyle X\,\!}$ je bod, který leží v rovině a vektory ${\displaystyle u\,\!}$ a ${\displaystyle v\,\!}$ jsou nekolineární vektory ležící v rovině, tzn. jsou to směrové vektory roviny.

Úseková rovnice roviny

Úsekovou rovnici roviny zapisujeme jako

${\displaystyle {\frac {x}{p}}+{\frac {y}{q}}+{\frac {z}{r}}=1}$,

kde ${\displaystyle p,\,q,\,r}$ vymezují úseky vyťaté rovinou na osách ${\displaystyle x,\,y,\,z\,\!}$.

Srovnáním úsekové a obecné rovnice dostáváme ${\displaystyle p=-{\frac {d}{a}},\,q=-{\frac {d}{b}},\,r=-{\frac {d}{c}}\,\!}$.

Normálová rovnice roviny

Normálová rovnice roviny má tvar

${\displaystyle x\cos \alpha +y\cos \beta +z\cos \gamma +p=0\,\!}$,

kde ${\displaystyle p\,\!}$ je vzdálenost počátku souřadného systému od roviny, tj. délka normály od počátku souřadnicového systému do průsečíku s rovinou,
${\displaystyle \cos \alpha ,\,\cos \beta ,\,\cos \gamma \,\!}$ jsou směrové kosiny roviny,
${\displaystyle \alpha ,\,\beta ,\,\gamma \,\!}$ představují úhly, které svírají kladné souřadnicové poloosy s normálou roviny.
Normála je směrnice kolmá ve všech směrech k rovině.
Směrové kosiny lze vyjádřit z obecné rovnice jako

${\displaystyle \cos \alpha ={\frac {a}{\varepsilon {\sqrt {a^{2}+b^{2}+c^{2}}}}}}$

${\displaystyle \cos \beta ={\frac {b}{\varepsilon {\sqrt {a^{2}+b^{2}+c^{2}}}}}}$

${\displaystyle \cos \gamma ={\frac {c}{\varepsilon {\sqrt {a^{2}+b^{2}+c^{2}}}}}}$

kde ${\displaystyle \varepsilon =1\,\!}$ pro ${\displaystyle \operatorname {sgn}(p)=-1\,\!}$ a pro ${\displaystyle \varepsilon =-1\,\!}$ pro ${\displaystyle \operatorname {sgn}(p)=1\,\!}$.

Rovinný řez

Rovinným řezem geometrického útvaru ${\displaystyle U}$ rovinou ${\displaystyle \rho }$ se nazývá průnik roviny ${\displaystyle \rho }$ a útvaru ${\displaystyle U}$.

Rovinný řez plochy rovinou, ve které leží normála plochy, se nazývá normálovým řezem plochy.

Další informace

V mechanice a technice existují rovinné úlohy, tj. jestliže lze idealizovat těleso či technikou konstrukci tak, že leží a v jedné rovině. V této rovině také působí všechna zatížení. Příkladem mohou být např. rovinné příhradové konstrukce, rovinný ohyb nebo úlohy rovinné napjatosti či rovinné deformace.

Literatura

• Marcela Palková a kolektiv: Průvodce matematikou 2, Didaktis, Brno 2007, ISBN 978-80-7358-083-4, str. 107-109

Související články

• Geometrie
• Základní geometrické útvary
• Polorovina
• Vzájemná poloha bodu a roviny
• Vzájemná poloha rovin
• Vzájemná poloha přímky a roviny

Externí odkazy

• Obrázky, zvuky či videa k tématu rovina na Wikimedia Commons
• Téma Rovina ve Wikicitátech
• Slovníkové heslo rovina ve Wikislovníku

Tento článek je příliš stručný nebo postrádá důležité informace. Pomozte Wikipedii tím, že jej vhodně rozšíříte. Nevkládejte však bez oprávnění cizí texty.