Różnica zbiorów

Różnica zbiorów ${\displaystyle A}$ i ${\displaystyle B}$ – podzbiór zbioru ${\displaystyle A}$ złożony z tych elementów, które nie należą do ${\displaystyle B,}$ oznaczany ${\displaystyle A\setminus B}$ – ukośnikiem wstecznym^[1][2][3], niekiedy także minusem: ${\displaystyle A-B}$^[4][5][6]. Formalnie^[4][5][6]:

${\displaystyle x\in (A\setminus B)\Leftrightarrow (x\in A)\land (x\notin B),}$

co jest równoważne

${\displaystyle A\setminus B=\{x\in \Omega \;:\;x\in A\land x\notin B\}}$^[2]${\displaystyle {}=\{x\in A\;:\;x\notin B\}}$^[3],

gdzie ${\displaystyle \Omega }$ jest zbiorem wszystkich rozważanych elementów zwanym przestrzenią^[7][8] lub uniwersum^[9].

Za pomocą różnicy zbiorów można zdefiniować dwie inne operacje: różnicę symetryczną i dopełnienie zbioru.

Przykłady

• Niech ${\displaystyle \mathbb {Q} }$ będzie zbiorem liczb wymiernych, a ${\displaystyle \mathbb {R} }$ niech będzie zbiorem liczb rzeczywistych. Wówczas ${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$ jest zbiorem liczb niewymiernych^[4] ${\displaystyle \mathbb {I} \mathbb {Q} {:}}$

${\displaystyle \mathbb {R} \setminus \mathbb {Q} =\mathbb {I} \mathbb {Q} .}$

• Jeżeli ${\displaystyle A=\{a,b,c\},}$ a ${\displaystyle B=\{b,c,d\},}$ to ${\displaystyle A\setminus B=\{a\}.}$

Własności

Ogólne

Różnica zbiorów:

• nie jest przemienna – w ogólności ${\displaystyle A\backslash B\neq B\backslash A;}$
• nie jest łączna – w ogólności ${\displaystyle (A\backslash B)\backslash C\neq A\backslash (B\backslash C);}$ przykładowo ${\displaystyle (A\backslash A)\backslash A=\emptyset \backslash A=\emptyset ,A\backslash (A\backslash A)=A\backslash \emptyset =A;}$
• ma jeden idempotent: ${\displaystyle A\backslash A=A\Rightarrow \emptyset =A;}$
• ma prawostronny element neutralny: ${\displaystyle A\backslash \emptyset =A;}$
• ma lewostronny element absorbujący: ${\displaystyle \emptyset \backslash A=\emptyset .}$

Związki z inkluzją

${\displaystyle A}$ jest podzbiorem ${\displaystyle B}$ (czyli zbiór ${\displaystyle A}$ zawiera się w ${\displaystyle B}$) wtedy i tylko wtedy, gdy różnica ${\displaystyle A\backslash B}$ jest zbiorem pustym:

${\displaystyle A\subseteq B\Leftrightarrow A\setminus B=\varnothing .}$

Z inkluzji dwóch par zbiorów można wywnioskować inkluzję pewnych różnic^[10][11]:

${\displaystyle A\subseteq B\land C\subseteq D\Rightarrow A\backslash D\subseteq B\backslash C.}$

Definicja przekroju

Za pomocą różnicy można zdefiniować także przekrój (część wspólną) zbiorów:

${\displaystyle A\cap B=A\setminus (A\setminus B)}$^[12].

• Dowód:

${\displaystyle x\in A\setminus (A\setminus B)\Leftrightarrow (x\in A)\wedge \neg [x\in (A\setminus B)]\Leftrightarrow (x\in A)\wedge \neg [(x\in A)\wedge \neg (x\in B)]\Leftrightarrow }$

${\displaystyle (x\in A)\wedge [\neg (x\in A)\vee (x\in B)]\Leftrightarrow [(x\in A)\wedge \neg (x\in A)]\vee [(x\in A)\wedge (x\in B)]\Leftrightarrow }$

${\displaystyle (x\in A)\wedge (x\in B)\Leftrightarrow x\in A\cap B\ \blacksquare }$

Prawa rozdzielności

Różnica zbiorów jest prawostronnie rozdzielna względem sumy zbiorów^[13]:

${\displaystyle (A\cup B)\backslash C=(A\backslash C)\cup (B\backslash C).}$

Iloczyn kartezjański jest rozdzielny względem różnicy zbiorów^[14]:

${\displaystyle A\times (B\backslash C)=(A\times B)\backslash (A\times C).}$

Prawa De Morgana i dualności

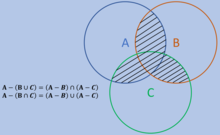
Różnica zbiorów nie jest rozdzielna lewostronnie względem sumy ani przekroju zbiorów, ale zachodzą podobne równości, zaliczane do praw De Morgana^[10][11]:

${\displaystyle A\backslash (B\cup C)=(A\backslash B)\cap (A\backslash C);}$

${\displaystyle A\backslash (B\cap C)=(A\backslash B)\cup (A\backslash C).}$

W teorii zbiorów i jej zastosowaniach ważną rolę odgrywa tak zwana zasada dualności^[15], która jest oparta na dwóch następujących tożsamościach:

• Dopełnienie sumy zbiorów jest równe iloczynowi ich dopełnień:

${\displaystyle X\setminus \bigcup \limits _{i}A_{i}=\bigcap \limits _{i}(X\setminus A_{i}).}$

• Dopełnienie iloczynu zbiorów jest równe sumie ich dopełnień:

${\displaystyle X\setminus \bigcap \limits _{i}A_{i}=\bigcup \limits _{i}(X\setminus A_{i}).}$

Zasada dualności w teorii mnogości polega na tym, że z dowolnej równości, dotyczącej podzbiorów ustalonego zbioru ${\displaystyle X}$ można całkiem automatycznie uzyskać równość dualną, zastępując wszystkie zbiory ich dopełnieniami, sumy – iloczynami, a iloczyny – sumami.

Przypisy

Zobacz podręcznik w Wikibooks: Matematyka dla liceum – Liczby i ich zbiory

Bibliografia

• A.N. Kołmogorow, S.W. Fomin: Elementy teorii funkcji i analizy funkcjonalnej (wyd. ros.). Wyd. 2. Nauka, 1989. ISBN 5-02-013993-9.
• Kazimierz Kuratowski, Andrzej Mostowski: Teoria mnogości. Warszawa: Polskie Towarzystwo Matematyczne, 1952, seria: Monografie matematyczne, t. 27. OCLC 250182901. [dostęp 2016-09-23].
• Kazimierz Kuratowski: Wstęp do teorii mnogości i topologii. Wyd. 5. Warszawa: Państwowe Wydawnictwo Naukowe, 1972, seria: Biblioteka Matematyczna.
• Kazimierz Kuratowski: Wstęp do teorii mnogości i topologii. Wyd. 8. Warszawa: PWN, 1980, seria: Biblioteka Matematyczna, t. 9. ISBN 83-01-01372-9.
• Roman Leitner: Zarys matematyki wyższej dla studentów. Wyd. 11. Cz. 1. Warszawa: WNT, 1999. ISBN 83-204-2395-3.
• Zdzisław Opial: Algebra wyższa. PWN, 1972.
• Helena Rasiowa: Wstęp do matematyki współczesnej. Wyd. 5. Warszawa: PWN, 1975, seria: Biblioteka Matematyczna, t. 30. OCLC 749626864.
• Helena Rasiowa: Wstęp do matematyki współczesnej. Wyd. 14. Warszawa: PWN, 2004. ISBN 83-01-14294-4.
• Kenneth A. Ross, Charles R.B Wright: Matematyka dyskretna. E. Sepko-Guzicka (tłum.), W. Guzicki (tłum.), P. Zakrzewski (tłum.). Warszawa: Wydawnictwo Naukowe PWN, 1996. ISBN 83-01-12129-7.

Linki zewnętrzne

• Szymon Charzyński, Różnica zbiorów, kanał Khan Academy Po Polsku na YouTube, 24 września 2013 [dostęp 2023-09-07].