Loi de Rice

Pour les articles homonymes, voir Rice.

Rice
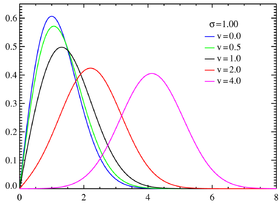Densité de probabilité pour différentes valeurs de ν   avec σ = 1. pour différentes valeurs de ν   avec σ = 0,25.
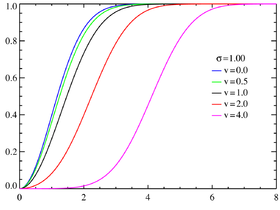Fonction de répartition avec σ = 1,0 pour différentes valeurs de ν. avec σ = 0,25 pour différentes valeurs de ν.
Paramètres	${\displaystyle \nu \geq 0\,}$ ${\displaystyle \sigma \geq 0\,}$
Support	${\displaystyle x\in [0;\infty )}$
Densité de probabilité	${\displaystyle {\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)}$
Fonction de répartition	${\displaystyle 1-Q_{1}\left({\frac {\nu }{\sigma }},{\frac {x}{\sigma }}\right)}$ où ${\displaystyle Q_{1}}$ est la fonction Q de Marcum
Espérance	${\displaystyle \sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})}$
Variance	${\displaystyle 2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{1/2}^{2}\left({\frac {-\nu ^{2}}{2\sigma ^{2}}}\right)}$
Asymétrie	(compliqué)
Kurtosis normalisé	(compliqué)
modifier

En statistiques et théorie des probabilités, la loi de Rice, nommée d'après Stephen O. Rice (en) (1907–1986), est une loi de probabilité à densité (c'est-à-dire continue).

C'est une généralisation de la loi de Rayleigh utilisée pour décrire le comportement d'un signal radio qui se propage selon plusieurs chemins (multipath) avant d'être reçu par une antenne.

Caractérisation

Soient deux variables de Gauss centrées, indépendantes, de même variance σ². Si on considère qu'elles représentent les deux coordonnées d'un point d'un plan, la distance de ce point à l'origine suit une loi de Rayleigh :

${\displaystyle f(x,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}$.

En supposant que la distribution est centrée sur un point de coordonnées (ν cos θ, ν sin θ) (coordonnées polaires (ν , θ)), la densité de probabilité devient :

${\displaystyle f(x|\nu ,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)}$

où I₀(z) est la fonction de Bessel modifiée de première espèce et d'ordre 0.

Propriétés

Moments

Les premiers moments (non centrés) sont :

${\displaystyle \mu _{1}=\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})}$

${\displaystyle \mu _{2}=2\sigma ^{2}+\nu ^{2}\,}$

${\displaystyle \mu _{3}=3\sigma ^{3}{\sqrt {\pi /2}}\,\,L_{3/2}(-\nu ^{2}/2\sigma ^{2})}$

${\displaystyle \mu _{4}=8\sigma ^{4}+8\sigma ^{2}\nu ^{2}+\nu ^{4}\,}$

${\displaystyle \mu _{5}=15\sigma ^{5}{\sqrt {\pi /2}}\,\,L_{5/2}(-\nu ^{2}/2\sigma ^{2})}$

${\displaystyle \mu _{6}=48\sigma ^{6}+72\sigma ^{4}\nu ^{2}+18\sigma ^{2}\nu ^{4}+\nu ^{6}\,}$

${\displaystyle L_{\nu }(x)=L_{\nu }^{0}(x)=M(-\nu ,1,x)=\,_{1}F_{1}(-\nu ;1;x)}$

où, L_ν(x) représente un polynôme de Laguerre et M désigne la fonction hypergéométrique confluente.

Pour le cas ν = 1/2 :

${\displaystyle L_{1/2}(x)=\,_{1}F_{1}\left(-{\frac {1}{2}};1;x\right)}$

${\displaystyle =\mathrm {e} ^{x/2}\left[\left(1-x\right)I_{0}\left({\frac {-x}{2}}\right)-xI_{1}\left({\frac {-x}{2}}\right)\right].}$

Généralement les moments sont donnés par

${\displaystyle \mu _{k}=s^{k}2^{k/2}\,\Gamma (1\!+\!k/2)\,L_{k/2}(-\nu ^{2}/2\sigma ^{2}),\,}$

où s = σ^1/2.

Lorsque k est pair, les moments deviennent des polynômes en σ et ν.

Distributions liées

• La variable ${\displaystyle r={\sqrt {x^{2}+y^{2}}}}$ suit une loi de Rice ${\displaystyle R\sim \mathrm {Rice} \left(\sigma ,\nu \right)}$ à condition que ${\displaystyle X\sim {\mathcal {N}}\left(\nu \cos \theta ,\sigma ^{2}\right)}$ et ${\displaystyle Y\sim {\mathcal {N}}\left(\nu \sin \theta ,\sigma ^{2}\right)}$ soient deux variables gaussiennes indépendantes.
• Pour obtenir une variable ${\displaystyle R\sim \mathrm {Rice} \left(\nu ,\sigma \right)}$, on peut considérer une autre procédure :

1. Tirer P selon une loi de Poisson, de paramètre ${\displaystyle \lambda ={\frac {\nu ^{2}}{2\sigma ^{2}}}.}$
2. Tirer X selon une loi du χ² avec 2P + 2 degrés de liberté.
3. Poser R = σ √X.

• Si ${\displaystyle R\sim \mathrm {Rice} \left(1,\nu \right)}$ alors R² suit une loi du χ² non centrée, à 2 degrés de liberté et un paramètre de non-centralité ν².

Cas limites

Pour de grandes valeurs de l'argument, le polynôme de Laguerre devient^[1] :

${\displaystyle L_{\nu }(x)\ {\underset {x\rightarrow -\infty }{\sim }}\ {\frac {|x|^{\nu }}{\Gamma (1+\nu )}}.}$

On peut constater que lorsque ν devient grand ou que σ devient petit, alors la moyenne devient ν et la variance σ².

Notes et références

• (en) Stephen O. Rice, « Mathematical Analysis of Random Noise », dans Bell System Technical Journal, vol. 24, 1945, p. 46–156
• (en) I. Soltani Bozchalooi et Ming Liang, « A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection », dans Journal of Sound and Vibration, vol. 308, n^o 1-2, 2007, p. 246–267 DOI 10.1016/j.jsv.2007.07.038
• (en) John G. Proakis, Digital Communications, McGraw-Hill, 2000

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Rice distribution » (voir la liste des auteurs).

Liens externes

• (en) Le site SOCR fournit les ressources suivantes : interactive Rice distribution, Rice simulation, model-fitting and parameter estimation.
• (en) Multipath Reception pour la signification
• (en) Complex Gaussian distribution pour l'aspect mathématique
• (en) MATLAB code for Rice distribution (densité de probabilité, moyenne, variance et génération de nombres aléatoires)

• Portail des probabilités et de la statistique