Loi log-logistique

Le fond de cet article de mathématiques est à vérifier (décembre 2016).

Améliorez-le ou discutez des points à vérifier. Si vous venez d’apposer le bandeau, merci d’indiquer ici les points à vérifier.

Log-logistique
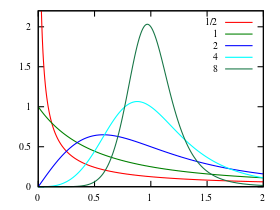Densité de probabilité Pour α = 1 et β en légende
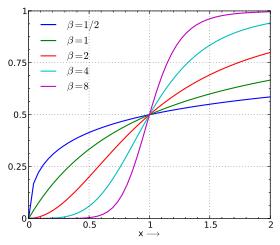Fonction de répartition α = 1 et β en légende
Paramètres	α > 0 échelle β > 0 forme
Support	${\displaystyle x\in [0,\infty )}$
Densité de probabilité	${\displaystyle {\frac {(\beta /\alpha )(x/\alpha )^{\beta -1}}{\left[1+(x/\alpha )^{\beta }\right]^{2}}}}$
Fonction de répartition	${\displaystyle {1 \over 1+(x/\alpha )^{-\beta }}}$
Espérance	${\displaystyle {\alpha \,\pi /\beta \over \sin(\pi /\beta )}}$ si β > 1, sinon pas définie
Médiane	α
Mode	${\displaystyle \alpha \left({\frac {\beta -1}{\beta +1}}\right)^{1/\beta }}$ si β > 1, 0 sinon
Variance	voir développement
modifier

Dans la théorie des probabilités et en statistiques, la loi log-logistique (connue aussi comme la distribution de Fisk en économie) est une loi de probabilité continue pour une variable aléatoire strictement positive. Elle est utilisée dans l'étude de la durée de vie d'événement dont l'intensité augmente d'abord pour ensuite décroître, comme pour la mortalité dû au cancer après diagnostic ou traitement. Elle est aussi utilisée en hydrologie pour modéliser le débit d'un cours d'eau ou le niveau des précipitations, et en économie pour modéliser l'inégalité des revenus.

La loi log-logistique est la loi d'une variable aléatoire dont le logarithme est distribué selon une loi logistique. Elle ressemble beaucoup à la loi log-normale, mais s'en distingue par des queues plus épaisses. Par ailleurs, sa fonction de répartition admet une expression explicite, contrairement à la log-normale.

Caractéristiques

Il existe différentes paramétrisations de la distribution. Celle choisie ici permet une interprétation raisonnable des paramètres et permet une expression simplifiée pour la fonction de répartition^[1],[2]. Le paramètre α > 0 est un paramètre d'échelle et joue aussi le rôle de médiane de la distribution. Le paramètre β > 0 est un paramètre de forme. La distribution est unimodale lorsque β > 1 et sa dispersion décroît lorsque β augmente.

La fonction de répartition est

${\displaystyle {\begin{aligned}F(x;\alpha ,\beta )&={1 \over 1+(x/\alpha )^{-\beta }}\\&={(x/\alpha )^{\beta } \over 1+(x/\alpha )^{\beta }}\\&={x^{\beta } \over \alpha ^{\beta }+x^{\beta }}\end{aligned}}}$

où ${\displaystyle x>0}$, α > 0, β > 0.

La densité de probabilité est

${\displaystyle f(x;\alpha ,\beta )={\frac {(\beta /\alpha )(x/\alpha )^{\beta -1}}{\left[1+(x/\alpha )^{\beta }\right]^{2}}}}$.

Propriétés

Moments

Le ${\displaystyle k}$-ième moment existe seulement quand ${\displaystyle k<\beta ,}$ et se donne alors par^[3],[4]

${\displaystyle {\begin{aligned}\operatorname {E} (X^{k})&=\alpha ^{k}\,\operatorname {B} (1-k/\beta ,\,1+k/\beta )\\&=\alpha ^{k}\,{k\,\pi /\beta \over \sin(k\,\pi /\beta )}\end{aligned}}}$

où B est la fonction bêta. L'expression pour les espérance, variance, coefficient d'asymétrie et coefficient d’aplatissement (kurtosis) se tirent de l'expression précédente. En posant ${\displaystyle b=\pi /\beta ,}$ la moyenne prend la forme

${\displaystyle \operatorname {E} (X)=\alpha b/\sin b,\quad \beta >1}$

et la variance devient

${\displaystyle \operatorname {Var} (X)=\alpha ^{2}\left(2b/\sin 2b-b^{2}/\sin ^{2}b\right),\quad \beta >2}$.

Les expressions explicites de la kurtosis et du skewness sont plus longues à reproduire^[5]. Lorsque β tend vers l'infini, la moyenne (espérance) tend vers α, la variance et le skewness tendent tous deux vers 0 et la kurtosis tend vers 6/5 (voir aussi #Distributions associées ci-dessous).

Quantiles

L'inverse de la fonction de répartition est donnée par :

${\displaystyle F^{-1}(p;\alpha ,\beta )=\alpha \left({\frac {p}{1-p}}\right)^{1/\beta }}$.

Il s'ensuit que la médiane est α, le premier quartile est ${\displaystyle 3^{1/\beta }\alpha }$ et le dernier quartile est ${\displaystyle 3^{-1/\beta }\alpha }$.

Applications

Analyse de survie

La distribution log-logistique procure un modèle paramétrique pour l'analyse de survie (durée de vie). Contrairement à l'habituelle distribution de Weibull, cette densité permet une fonction de risque (défaillance) non monotone : lorsque β > 1, la fonction de risque est unimodale (lorsque β ≤ 1, le risque décroît de manière monotone). Le fait de disposer d'une expression explicite pour la fonction de répartition est un avantage pour l'analyse de survie avec des données tronquées (ou censurées)^[6].

La fonction de survie est donnée par :

${\displaystyle S(t)=1-F(t)=\left[1+\left({\frac {t}{\alpha }}\right)^{\beta }\right]^{-1}}$

la fonction de risque :

${\displaystyle h(t)={\frac {f(t)}{S(t)}}={\frac {{\dfrac {\beta }{\alpha }}\left({\dfrac {t}{\alpha }}\right)^{\beta -1}}{1+\left({\dfrac {t}{\alpha }}\right)^{\beta }}}}$

et la fonction de risque cumulé :

${\displaystyle H(t)=-\log(S(t))=\log \left[1+\left({\frac {t}{\alpha }}\right)^{\beta }\right]}$

Hydrologie

La distribution log-logistique a permis de modéliser le débit des cours d'eau ou encore les précipitations.

Économie

La distribution log-logistique permet en sciences économiques de modéliser simplement les inégalités de revenu, souvent sous la dénomination de « distribution de Fisk »^[7]. Son coefficient de Gini est ${\displaystyle 1/\beta }$^[8].

Distributions associées

• Si X a une distribution log-logistique avec pour paramètre d'échelle α et pour paramètre de forme β alors Y = log(X) est distribué selon une loi logistique, avec pour paramètre de position log(α) et pour paramètre d'échelle 1/β.
• Lorsque le paramètre de forme β augmente, la distribution log-logistique s'approche de plus en plus d'une distribution logistique. Ou, de manière informelle, lorsque ${\displaystyle \beta \to \infty }$,

  ${\displaystyle LL(\alpha ,\beta )\to L(\alpha ,\alpha /\beta )}$.

• La distribution log-logistique LL(β = 1, α) est identique à une distribution de Pareto généralisée, de paramètre de position ${\displaystyle \mu =0}$, de paramètre de forme ${\displaystyle \xi =1}$ et de paramètre d'échelle α :

${\displaystyle LL(\alpha ,1)=GPD(1,\alpha ,1)}$.

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Notes et références

• Portail des probabilités et de la statistique