Loi de Slash

Cet article est une ébauche concernant les probabilités et la statistique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Loi de Slash
Densité de probabilité
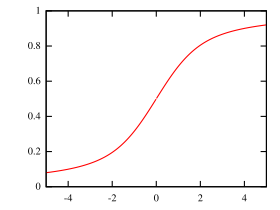Fonction de répartition
Paramètres	aucun
Support	${\displaystyle x\in \,]-\infty ;+\infty [\!~}$
Densité de probabilité	${\displaystyle {\frac {\varphi (0)-\varphi (x)}{x^{2}}}}$
Fonction de répartition	${\displaystyle {\begin{cases}\Phi (x)-{\frac {\varphi (0)-\varphi (x)}{x}}&{\text{si}}\,x\neq 0\\1/2&{\text{si}}\,x=0\\\end{cases}}}$
Espérance	n'existe pas
Médiane	0
Mode	0
Variance	n'existe pas
Asymétrie	n'existe pas
Kurtosis normalisé	n'existe pas
Fonction génératrice des moments	n'existe pas
Fonction caractéristique	${\displaystyle {\sqrt {2\pi }}{\Big (}\varphi (t)+t\Phi (t)-\max\{t,0\}{\Big )}}$
modifier

En théorie des probabilités, la loi de Slash est la loi de probabilité d'une variable aléatoire de loi normale divisée par une variable aléatoire de loi uniforme continue^[1],[2]. En d'autres termes, si ${\displaystyle Z}$ est une variable normale centrée réduite (moyenne est nulle et la variance vaut 1), si ${\displaystyle U}$ est uniforme sur ${\displaystyle [0,1]}$ et si ${\displaystyle Z}$ et ${\displaystyle U}$ sont indépendantes alors la variable ${\textstyle X={\frac {Z}{U}}}$ suit une loi de Slash. Cette loi a été nommée ainsi par William H. Rogers (en) et John Tukey dans un article publié en 1972^[3].

Fonction de densité

Sa fonction de densité est donnée par

${\displaystyle f(x)={\frac {\varphi (0)-\varphi (x)}{x^{2}}}}$

où ${\displaystyle \varphi }$ est la fonction de densité d'une loi normale centrée réduite. Elle n'est pas définie pour ${\displaystyle x=0}$, mais cette valeur interdite est remplacée par :

${\displaystyle \lim _{x\rightarrow 0}f(x)={\frac {\phi (0)}{2}}={\frac {1}{2{\sqrt {2\pi }}}}}$

L'utilisation la plus commune de la loi de Slash est dans l'étude de simulations. Cette loi possède une queue plus lourde que la loi normale mais n'est cependant pas pathologique comme la loi de Cauchy^[4].

Généralisation

Plus récemment, le terme de loi Slash désigne la loi de toute variable de la forme ${\textstyle X=Z/U^{\frac {1}{q}}}$, où Z et U sont deux variables indépendantes, U suit une loi uniforme sur [0;1] et q > 0. Par extension, U peut aussi être choisi comme une variable suivant une loi bêta ; on parle alors de beta divided slash distribution^[5].

Références

• Portail des probabilités et de la statistique